I - In the previous two posts we discussed MSK performance in an AWGN channel, first presenting the MATLAB/OCTAVE Code for one sample per symbol case [Post 1], and then extending it to the more general case of multiple samples per symbol [Post 2]. This helps us visualize the underlying beauty of Continuous Phase Modulation (CPM) which reduces out of band energy and consequently lowers Adjacent Channel Interference (ACI). We also briefly touched upon the case of MSK in Rayleigh fading, but did not go into the details. So here we take a deeper dive.Continue reading MSK Bit Error Rate in Rayleigh Fading
Category Archives: BER Performance
MSK – A Continuous Phase Modulation (CPM)
Some Background on MSK
I – In the previous post we presented the mathematical model and code for BER calculation of a popular modulation scheme called MSK. However in the code we shared, we only considered one sample per symbol, which makes MSK look like BPSK. While BPSK symbols fall on the real axis, MSK symbols alternate between real and imaginary axes, progressing by π/2 phase during each symbol period. MSK signal thus has memory and this can help in demodulation using advanced techniques such as Viterbi Algorithm.Continue reading MSK – A Continuous Phase Modulation (CPM)
Minimum Shift Keying Bit Error Rate in AWGN
I - Minimum Shift Keying (MSK) is a type of Continuous Phase Modulation (CPM) that has been used in many wireless communication systems. To be more precise it is Continuous Phase Frequency Shift Keying (CPFSK) with two frequencies f1 and f2. The frequency separation between the two tones is the minimum allowable while maintaining orthogonality and is equal to half the bit rate (or symbol rate, as both are the same). The frequency deviation is then given as Δf=Rb/4. The two tones have frequencies of fc±Δf where fc is the carrier frequency. MSK is sometimes also visualized as Offset QPSK (OQPSK) but we will not go into its details here.Continue reading Minimum Shift Keying Bit Error Rate in AWGN
Pulse Amplitude Modulation Symbol Error Rate in AWGN
Pulse Amplitude Modulation (PAM) is a one dimensional or in other words real modulation. Simply put it is an extension of BPSK with M amplitude levels instead of two. This can be a bit confusing because BPSK can be looked at as a phase modulation and its natural extension must be QPSK or 8-PSK modulations. To remove this ambiguity lets call M-PAM an extension of simple amplitude modulation but with M levels. In the discussion below we consider M=4 but then extend it to the general case of M=2k (k=1,2,3…).
Continue reading Pulse Amplitude Modulation Symbol Error Rate in AWGNMassive MIMO and Antenna Correlation
Some Background
In a previous post we calculated the Bit Error Rate (BER) of a Massive MIMO system using two different channel models namely deterministic and probabilistic. The deterministic channel model is derived from the geometry of the array (ULA in this case) and the distribution of users in the cell. Whereas probabilistic channel model assumes that the channel is flat fading and can be modeled, between each transmit receive pair, as a complex, circularly symmetric, Gaussian random variable with mean of zero and variance of 0.5 per dimension.
Continue reading Massive MIMO and Antenna CorrelationMassive MIMO Fundamentals and Code
Background
Just like different frequency bands and time slots can be used to multiplex users, spatial domain can also be exploited to achieve the same result. It is well known that if there are 4 transmit antennas and 4 receive antennas then four simultaneous data streams can be transmitted over the air. This can be scaled up to 8 x 8 or in the extreme case to 128 x 128. When the number of transmit or receive antennas is greater than 100 we typically call it a Massive MIMO scenario and we need specialized signal processing techniques to handle this case. Computationally complex techniques like Maximum Likelihood (ML) become quite difficult to implement in real-time and we have to resort to some simplified linear array processing techniques. This is the topic of this blog post.
Description of the Scenario
To understand the scenario that we will discuss here, please look at our previous post. Also note that when we talk about nT x nR case we do not necessarily mean nT transmit antennas and nR receive antennas, it could also mean nT users with 1 antenna each and co-located nR receive antennas, such as at a base station. We typically assume that the number of receive antennas is greater than the number of users. When the number of users is greater than the number of receive antennas we call it overloaded case and this is not discussed here. Here the number of users is fixed at 16 (randomly distributed between 0 and 360 degrees within the cell) and the number of receive antennas is varied from 20 to 100.
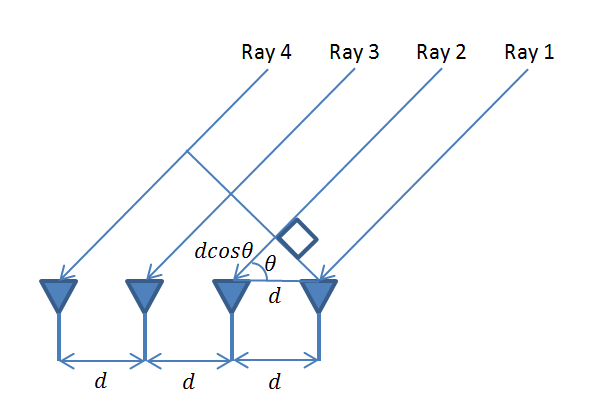
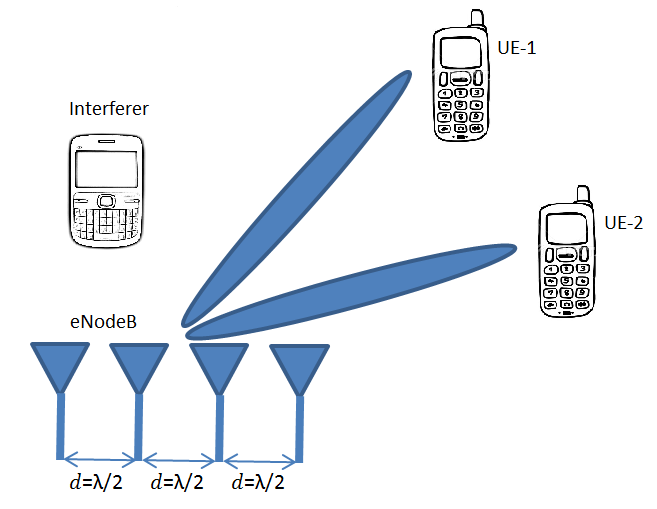
Linear Signal Processing Techniques for Massive MIMO
The four signal processing techniques that are applied at the receive array are:
- Matched Filtering (MF)
- Moore Penrose Pseudo-Inverse without controlling the threshold (PINV)
- Moore Penrose Pseudo-Inverse with a specified threshold (PINV with tol)
- Minimum Mean Squared Error (MMSE)
Simulation Results
There are some other techniques that we experimented with but are omitted here for the sake of brevity. The MATLAB code and simulation results showing bit error rate as a function of receive array size (nR) are given below. It is seen that simple Matched Filter works quite well when the receive array size is small but with increasing nR the performance improvement is not that great. Least Squares (LS) technique using Moore-Penrose Pseudo Inverse shows improved performance with increasing nR and this can be further improved by controlling the threshold (tol). We found that a threshold of 0.1 gave significantly improved results as compared to no threshold case. Lastly we implemented MMSE and found that it gave us the best results. It must be noted that we also implemented ML for a limited size of receive array and found that its BER performance was far superior than any other technique.
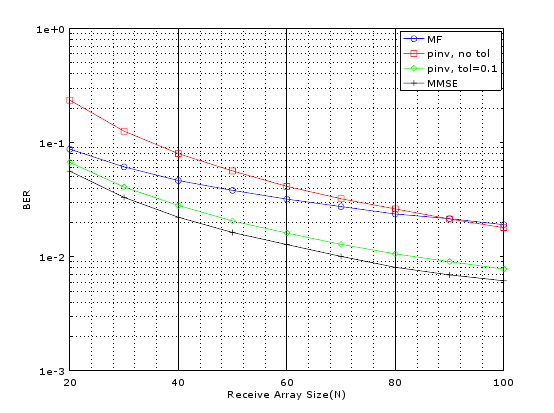
MATLAB Code for Massive MIMO Scenario
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% MASSIVE MIMO BEAMFORMING
% COPYRIGHT RAYMAPS (C) 2018
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clear all
close all
% SETTING THE PARAMETERS FOR THE SIMULATION
f=1e9; %Carrier frequency
c=3e8; %Speed of light
l=c/f; %Wavelength
d=l/2; %Rx array spacing
N=20; %Receive array size
M=16; %Transmit array size (users)
theta=2*pi*(rand(1,M)); %Angular separation of users
EbNo=10; %Energy per bit to noise PSD
sigma=1/sqrt(2*EbNo); %Standard deviation of noise
n=1:N; %Rx array number
n=transpose(n); %Row vector to column vector
% RECEIVE SIGNAL MODEL (LINEAR)
s=2*(round(rand(M,1))-0.5); %BPSK signal of length M
H=exp(-i*(n-1)*2*pi*d*cos(theta)/l); %Channel matrix of size NxM
wn=sigma*(randn(N,1)+i*randn(N,1)); %AWGN noise of length N
x=H*s+wn; %Receive vector of length N
% LINEAR ARRAY PROCESSING - METHODS
% 1-MATCHED FILTER
y=H'*x;
% 2-PINV without tol
% y=pinv(H)*x;
% 3-PINV with tol
% y=pinv(H,0.1)*x;
% 4-Minimum Mean Square Error (MMMSE)
% y=(H'*H+(2*sigma^2)*eye([M,M]))^(-1)*(H')*x;
% DEMODULATION AND BER CALCULATION
s_est=sign(real(y)); %Demodulation
ber=sum(s!=s_est)/length(s); %BER calculation
%Note: Please select the array processing technique
%you want to implement (1-MF, 2-LS1, 3-LS2, 4-MMSE)
Note:
- In the code above, N=nR and M=nT
- What is labelled here as Matched Filter (MF) is strictly speaking Maximal Ratio Combining (MRC)
- The case we discuss above is categorized as Multiuser MIMO (MU-MIMO) for the uplink
- MU-MIMO for the downlink is not that straight forward and will be the subject of some future post
- We have considered a deterministic channel model as opposed to a probabilistic channel model
- Probabilistic channel model can be easily implemented by assuming that channel coefficients are independent and identically distributed (IID) complex Gaussian random variables with mean zero and variance of 0.5 per dimension
- The initial results we have obtained using this probabilistic channel model are much better than the results shown above, but the question remains which is the more accurate representation of a real channel
Update: Simulation Using a Probabilistic Channel
Since most of the literature in Massive MIMO uses a probabilistic channel instead of a deterministic channel, we decided to investigate this further. To implement such a channel model we simply need to change one line of the MATLAB code shown above. Instead of defining H as:
H=exp(-i*(n-1)*2*pi*d*cos(theta)/l);
We define H as:
H=(1/sqrt(2))*randn(N,M)+i*(1/sqrt(2))*randn(N,M);
The results are shown below. It is seen that the BER performance is orders of magnitude better. We would next investigate the performance degradation if the channel coefficients are not independent and identically distributed (IID) but have some correlation. This is closely tied to inter-element separation of the antenna array.
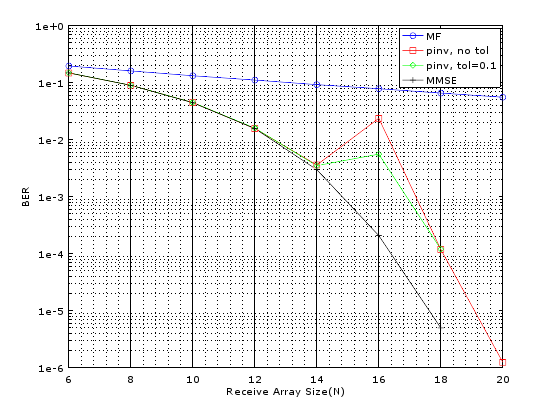
Concluding Remarks
The fundamental question that needs to be asked is why the performance in the NLOS scenario (probabilistic) is better than LOS scenario (deterministic). This has to do with the Signal to Noise Ratio [1]. In the above we have assumed the Signal to Noise Ratio (SNR) for the two scenarios to be the same. But realistically speaking this is never the case. Although the NLOS case assumes a rich scattering environment providing a high multiplexing gain (dependent on the rank of the channel matrix H) its SNR would always be lower due to reflection, diffraction and scattering loss. So a fair comparison between the LOS and NLOS case is only possible if we downward adjust the SNR for the NLOS case. Simulation results have shown that the SNR for the NLOS case needs to be downgraded by about 25 dB to have similar BER performance as the LOS case. Lastly it must be noted that the BER performance of the NLOS case would deteriorate once the channel coefficients are not IID and there is some correlation between them.
[1] Zimu Cheng, Binghao Chen, and Zhangdui Zhong “A Tradeoff between Rich Multipath and High Receive Power in MIMO Capacity”, International Journal of Antennas and Propagation, Volume 2013.