Recently I came across a post from T-Mobile in which they claim to have achieved a download speed of 5.6 Gbps over a 100 MHz channel resulting in a Spectral Efficiency of more than 50 bps/Hz. This was achieved in an MU-MIMO configuration with eight connected devices having an aggregate of 16 parallel streams i.e. two parallel streams per device. The channel used for this experiment was the mid-band frequency of 2.5 GHz.

Now let us revisit the Shannon Capacity theorem and see what data rate it predicts with the above parameters. Shannon Capacity theorem is given as:

C = N x BW x log2(1+SNR)

where

N=16 is the number of parallel streams enabled by multiple antennas at Tx and Rx

BW=100 MHz is the total bandwidth available to the carrier in the 2.5 GHz band

SNR=10 is the Signal to Noise Ratio (a moderately good SNR is assumed)

Plugging these numbers in, we get a capacity limit of 5.54 Gbps, approximately the same number obtained in the experiment. But it all depends upon the Signal to Noise Ratio, that has not been mentioned by T-Mobile in the reference post. With an SNR=20 dB, a very good channel condition, the capacity increases to about 10.65 Gbps but with an SNR=0 dB, a likely scenario at the cell edge, the capacity drops to 1.6 Gbps. The details for the capacity at different SNRs are given in the table and figure below.

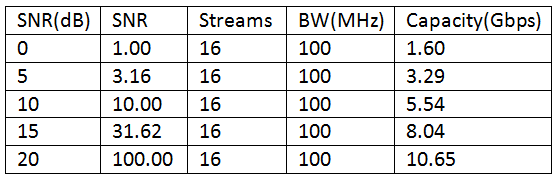
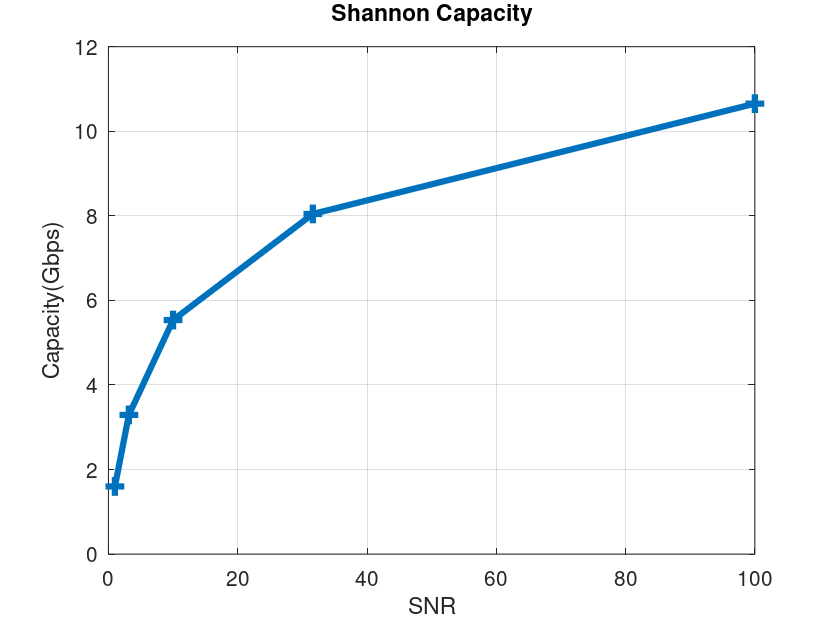
1. Please note that the above capacity calculations are for eight users simultaneously connected over the 100 MHz channel. The data rate achieved by a single user, in the T-Mobile experiment, was 5600/8=700 Mbps.
2. Also note that much higher bandwidths are available in the millitmeter wave band and this may increase the data rates 10 fold or even higher.

References:

https://www.t-mobile.com/news/network/t-mobile-achieves-mind-blowing-5g-speeds-with-mu-mimo

https://www.waveform.com/a/b/guides/5g-and-shannons-law

Author: Yasir Ahmed (aka John)

More than 20 years of experience in various organizations in Pakistan, the USA, and Europe. Worked as a Research Assistant within the Mobile and Portable Radio Group (MPRG) of Virginia Tech and was one of the first researchers to propose Space Time Block Codes for eight transmit antennas. The collaboration with MPRG continued even after graduating with an MSEE degree and has resulted in 12 research publications and a book on Wireless Communications. Worked for Qualcomm USA as an Engineer with the key role of performance and conformance testing of UMTS modems. Qualcomm is the inventor of CDMA technology and owns patents critical to the 4G and 5G standards.

Twitter Facebook Linkedin