In a previous post we have seen that MIMO fading capacity is much higher than AWGN capacity with multiple antennas. How is this possible? How can randomness added by a fading channel help us? In this post we try to find the reason for this. Let’s assume the following signal model for a Multi Input Multi Output antenna system.

x=Hs+w

Here s is the N_T by 1 signal vector, w is the N_R by 1 noise vector and H is the N_R by N_T channel matrix. The received signal vector is represented by x which has dimensions of N_R by 1. In expanded form this can be written as (assuming N_T =4 and N_R =4):

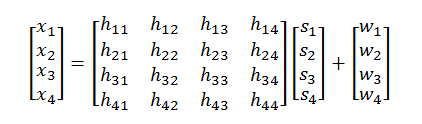
Let’s assume that there is no fading and all entries of the channel matrix are equal to unity i.e. the channel provides no gain or phase rotation. Let’s further assume that the four transmitted symbols are A, B, C and D (real modulation like PAM is assumed). Then in an AWGN channel we have:

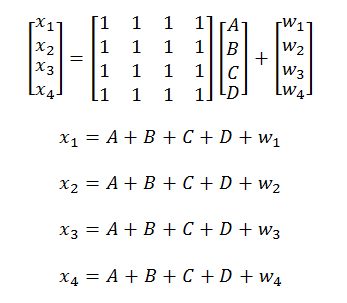
Let’s assume that A=1, B=3, C=5 and D=-1. Let’s further assume that there is no noise i.e. vector w is all zeros. The received signal vector x would then look like:

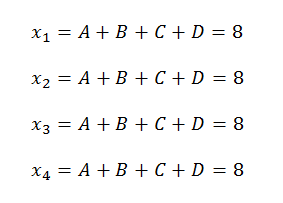
From linear algebra we know that to find four unknowns we need four independent equations. There is no way we can find the values of  A, B, C and D from the above equations. To simplify the above equations we have removed AWGN but even in presence of AWGN we will have the same predicament.

This shows that in the absence of fading there is no multiplexing gain however high the Signal to Noise Ratio is (in the above example SNR is infinite). Now let’s assume that we have a 4×4 MIMO fading channel, which might now look something like this (a totally random matrix that this author could think of):

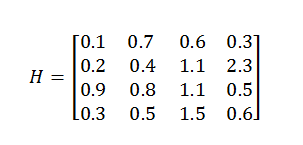
 Substituting in the above linear model we have:

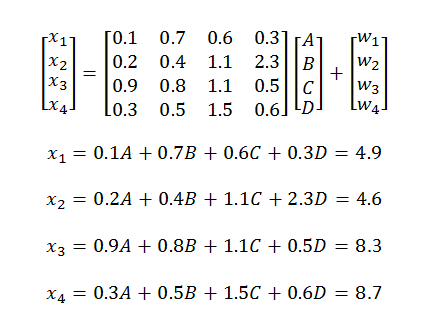
We have assumed that we are operating in the high SNR region where noise can be ignored. Now we have four nicely arranged linear independent equations that can be used to find four independent variables . So the fading channel does this magic to convert four dependent equations into four independent equations that can be easily solved (independence of equations can be checked by looking at the rank of channel matrix, which is 4 in this case).

There are a number of methods to solve the above system of equations but my preference is using matrix inversion using MATLAB function pinv (pseudo inverse). In case AWGN noise is added, the received vector x would deviate from the above and we might get some errors in estimation of the signal vector. Now looking back at the no fading case, we ask the question: is their a way to arrange the equations such that four variables A, B, C and D can be found?  

Author: Yasir Ahmed (aka John)

More than 20 years of experience in various organizations in Pakistan, the USA, and Europe. Worked as a Research Assistant within the Mobile and Portable Radio Group (MPRG) of Virginia Tech and was one of the first researchers to propose Space Time Block Codes for eight transmit antennas. The collaboration with MPRG continued even after graduating with an MSEE degree and has resulted in 12 research publications and a book on Wireless Communications. Worked for Qualcomm USA as an Engineer with the key role of performance and conformance testing of UMTS modems. Qualcomm is the inventor of CDMA technology and owns patents critical to the 4G and 5G standards.

Twitter Facebook Linkedin