I - In the previous two posts we discussed MSK performance in an AWGN channel, first presenting the MATLAB/OCTAVE Code for one sample per symbol case [Post 1], and then extending it to the more general case of multiple samples per symbol [Post 2]. This helps us visualize the underlying beauty of Continuous Phase Modulation (CPM) which reduces out of band energy and consequently lowers Adjacent Channel Interference (ACI). We also briefly touched upon the case of MSK in Rayleigh fading, but did not go into the details. So here we take a deeper dive.Continue reading MSK Bit Error Rate in Rayleigh Fading
Tag Archives: Rayleigh Fading
Wireless Channel Modeling: Back to Fundamentals
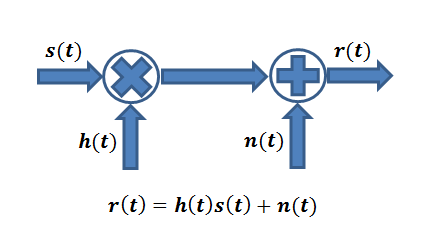
When a wireless signal travels from a transmitter (Tx) to a receiver (Rx) it undergoes some changes. In simple terms the signal s(t) is scaled by a factor h(t) and noise n(t) is added at the receiver. Let’s take this discussion forward with a simple example. Suppose the Tx transmits one of two possible symbols, +1 or -1. In technical lingo this is called Binary Phase Shift Keying (BPSK). If the channel scaling factor is 0.1 we will either get a +0.1 or -0.1 at the Rx to which AWGN noise is added. The noise is random in nature (having a Gaussian distribution) but for simplicity we assume that it can have one of two values, +0.01 or -0.01.
Continue reading Wireless Channel Modeling: Back to FundamentalsSum of Sinusoids Fading Simulator
We have previously looked at frequency domain fading simulators i.e. simulators that define the Doppler components in the frequency domain and then perform an IDFT to get the time domain signal. These simulators include Smith’s Simulator, Young’s Simulator and our very own Computationally Efficient Rayleigh Fading Simulator. Another technique that has been widely reported in the literature is Sum of Sinusoids Method. As the name suggests this method generates the Doppler components in the time domain and then sums them up to generate the time domain fading envelope. There are three parameters that define the properties of the generated signal.
1) Number of sinusoids – Higher the number better the properties of the generated signal but greater the computational complexity
2) Angle of arrival – This can be generated statistically or deterministically, spread from –pi to pi.
3) Phase of the arriving wave – This is uniformly distributed between –pi and pi.
The MATLAB code below gives three similar sum of sinusoids techniques for generating a Rayleigh faded envelope [1].
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% SUM OF SINUSOIDS FADING SIMULATORS
% fd - Doppler frequency
% fs - Sampling frequency
% ts - Sampling period
% N - Number of sinusoids
%
% www.raymaps.com
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clear all
close all
fd=70;
fs=1000000;
ts=1/fs;
t=0:ts:1;
N=100;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Method 1 - Clarke
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
x=zeros(1,length(t));
y=zeros(1,length(t));
for n=1:N;n
alpha=(rand-0.5)*2*pi;
phi=(rand-0.5)*2*pi;
x=x+randn*cos(2*pi*fd*t*cos(alpha)+phi);
y=y+randn*sin(2*pi*fd*t*cos(alpha)+phi);
end
z=(1/sqrt(N))*(x+1i*y);
r1=abs(z);
plot(t,10*log10(r1))
hold on
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Method 2 - Pop, Beaulieu
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
x=zeros(1,length(t));
y=zeros(1,length(t));
for n=1:N;n
alpha=2*pi*n/N;
phi=(rand-0.5)*2*pi;
x=x+randn*cos(2*pi*fd*t*cos(alpha)+phi);
y=y+randn*sin(2*pi*fd*t*cos(alpha)+phi);
end
z=(1/sqrt(N))*(x+1i*y);
r2=abs(z);
plot(t,10*log10(r2),'r')
hold on
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Method 3 - Chengshan Xiao
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
x=zeros(1,length(t));
y=zeros(1,length(t));
for n=1:N;n
phi=(rand-0.5)*2*pi;
theta=(rand-0.5)*2*pi;
alpha=(2*pi*n+theta)/N;
x=x+randn*cos(2*pi*fd*t*cos(alpha)+phi);
y=y+randn*sin(2*pi*fd*t*cos(alpha)+phi);
end
z=(1/sqrt(N))*(x+1i*y);
r3=abs(z);
plot(t,10*log10(r3),'g')
hold off
xlabel('Time(sec)')
ylabel('Envelope(dB)')
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
All the three techniques given above are quite accurate in generating a Rayleigh faded envelope with the desired statistical properties. The accuracy of these techniques increases as the number of sinusoids goes to infinity (we have tested these techniques with up to 1000 sinusoids but realistically speaking even 100 sinusoids are enough). If we want to compare the three techniques in terms of the Level Crossing Rate (LCR) and Average Fade Duration (AFD) we can say that the first and third technique are a bit more accurate than the second technique. Therefore we can conclude that a statistically distributed angle of arrival is a better choice than a deterministically distributed angle of arrival. Also, if we look at the autocorrelation of the in-phase and quadrature components we see that for the first and third case we get a zero order Bessel function of the first kind whereas for the second case we get a somewhat different sequence which approximates the Bessel function with increasing accuracy as the number of sinusoids is increased.
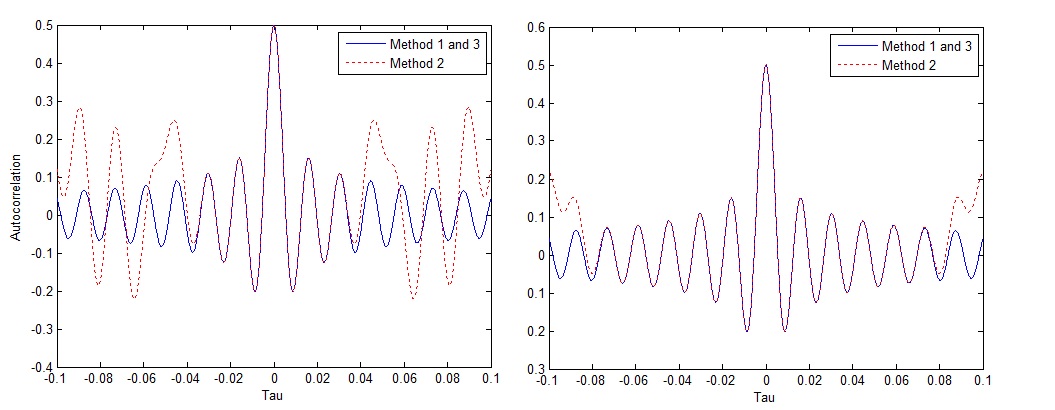
The above figures show the theoretical Bessel function versus the autocorrelation of the real/imaginary part generated by method number two. The figure on the left considers 20 sinusoids whereas the figure on the right considers 40 sinusoids. As can be seen the accuracy of the autocorrelation sequence increases considerably by doubling the number of sinusoids. We can assume that for number of sinusoids exceeding 100 i.e. N=100 in the above code the generated autocorrelation sequence would be quite accurate.
[1] Chengshan Xiao, “Novel Sum-of-Sinusoids Simulation Models for Rayleigh and Rician Fading Channels,” IEEE TRANSACTIONS ON WIRELESS COMMUNICATIONS, VOL. 5, NO. 12, DECEMBER 2006.
Uniform, Gaussian and Rayleigh Distribution
It is sometimes important to know the relationship between various distributions. This can be useful if there is a function available for one distribution and it can be used to derive other distributions. In the context of Wireless Communications it is important to know the relationship between the Uniform, Gaussian and Rayleigh distribution.
According to Central Limit Theorem the sum of a large number of independent and identically distributed random variables has a Gaussian distribution. This is used to model the amplitude of the in-phase and quadrature components of a wireless signal. Shown below is the model for the received signal which has been modulated by the Gaussian channel coefficients g1 and g2.
r=g1*a1*cos(2*pi*fc*t)+g2*a2*sin(2*pi*fc*t)
The envelope of this signal (sqrt(g1^2+g2^2)) as a Rayleigh distribution. Now if you only had a function for Uniform Distribution you can generate Rayleigh Distribution using the following routine.
clear all
close all
M=10000;
N=100;
for n=1:M;
x1=rand(1,N)-0.5;
x2=rand(1,N)-0.5;
y1=mean(x1);
y2=mean(x2);
z(n)=sqrt(y1^2+y2^2);
end
hist(z,20)
Note: Here a1 and a2 can be considered constants (at least during the symbol duration) and its really g1 and g2 that are varying.
Fading Model – From Simple to Complex
1. The simplest channel model just scales the input signal by a real number between 0 and 1 e.g. if the signal at the transmitter is s(t) then at the receiver it becomes a*s(t). The effect of channel is multiplicative (the receiver noise on the other hand is additive).
2. The above channel model ignores the phase shift introduced by the channel. A more realistic channel model is one that scales the input signal as well rotates it by a certain angle e.g. if s(t) is the transmitted signal then the received signal becomes a*exp(jθ)*s(t).
3. In a realistic channel the transmitter, receiver and/or the environment is in motion therefore the scaling factor and phase shift are a function of time e.g. if s(t) is the transmitted signal then the received signal is a(t)*exp(jθ(t))*s(t). Typically in simulation of wireless communication systems a(t) has a Rayleigh distribution and θ(t) has a uniform distribution.
4. Although the above model is quite popular, it can be further improved by introducing temporal correlation in the fading envelope. This can be achieved by the Smith’s simulator which uses a frequency domain approach to characterize the channel. The behavior of the channel is controlled by the Doppler frequency fd. Higher the Doppler frequency greater is the variation in the channel and vice versa [1].
5. Finally the most advanced wireless channel model is one that considers the channel to be an FIR filter where each tap is defined by the process outlined in (4). The channel thus performs convolution on the signal that passes through it. In the context of LTE there are three channel models that are defined namely Extended Pedestrian A (EPA), Extended Vehicular A (EVA) and Extended Typical Urban (UTU) [2].
Note: As an after thought I have realized that this channel model becomes even more complicated with the introduction of spatial correlation between the antennas of a MIMO system [3].
M-QAM Bit Error Rate in Rayleigh Fading
We have previously discussed the bit error rate (BER) performance of M-QAM in AWGN. We now discuss the BER performance of M-QAM in Rayleigh fading. The one-tap Rayleigh fading channel is generated from two orthogonal Gaussian random variables with variance of 0.5 each. The complex random channel coefficient so generated has an amplitude which is Rayleigh distributed and a phase which is uniformly distributed. As usual the fading channel introduces a multiplicative effect whereas the AWGN is additive.
The function “QAM_fading” has three inputs, ‘n_bits’, ‘M’, ‘EbNodB’ and one output ‘ber’. The inputs are the number of bits to be passed through the channel, the alphabet size and the Energy per Bit to Noise Power Spectral Density in dB respectively whereas the output is the bit error rate (BER).
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% FUNCTION THAT CALCULATES THE BER OF M-QAM IN RAYLEIGH FADING
% n_bits: Input, number of bits
% M: Input, constellation size
% EbNodB: Input, energy per bit to noise power spectral density
% ber: Output, bit error rate
% Copyright RAYmaps (www.raymaps.com)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function[ber]= QAM_fading(n_bits, M, EbNodB)
% Transmitter
k=log2(M);
EbNo=10^(EbNodB/10);
x=transpose(round(rand(1,n_bits)));
h1=modem.qammod(M);
h1.inputtype='bit';
h1.symbolorder='gray';
y=modulate(h1,x);
% Channel
Eb=mean((abs(y)).^2)/k;
sigma=sqrt(Eb/(2*EbNo));
w=sigma*(randn(n_bits/k,1)+1i*randn(n_bits/k,1));
h=(1/sqrt(2))*(randn(n_bits/k,1)+1i*randn(n_bits/k,1));
r=h.*y+w;
% Receiver
r=r./h;
h2=modem.qamdemod(M);
h2.outputtype='bit';
h2.symbolorder='gray';
h2.decisiontype='hard decision';
z=demodulate(h2,r);
ber=(n_bits-sum(x==z))/n_bits
return
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
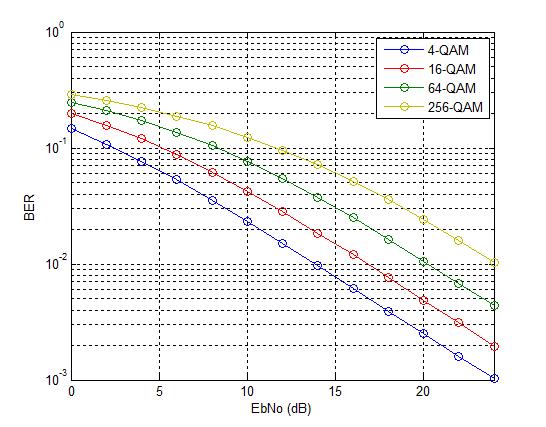
The bit error rates of four modulation schemes 4-QAM, 16-QAM, 64-QAM and 256-QAM are shown in the figure above. All modulation schemes use Gray coding which gives a few dB of margin in the BER performance. As with the AWGN case each additional bit per symbol requires about 1.5-2 dB in signal to ratio to achieve the same BER.
Although not shown here similar behavior is observed for higher order modulation schemes such as 1024-QAM and 4096-QAM (the gap in the signal to noise ratio for the same BER is increased to about 5dB).
Lastly we explain some of the terms used above.
Rayleigh Fading
Rayleigh Fading is a commonly used term in simulation of Digital Communication Systems but it tends to differ in meaning in different contexts. The term Rayleigh Fading as used above means a single tap channel that varies from one symbol to the next. It has an amplitude which is Rayleigh distributed and a phase which is Uniformly distributed. A single tap channel means that it does not introduce any Inter Symbol Interference (ISI). Such a channel is also referred to as a Flat Fading Channel. The channel can also be referred to as a Fast Fading Channel since each symbol experiences a new channel state which is independent of its previous state (also termed as uncorrelated).
Gray Coding
When using QAM modulation, each QAM symbol represents 2,3,4 or higher number of bits. That means that when a symbol error occurs a number of bits are reversed. Now a good way to do the bit-to-symbol assignment is to do it in a way such that no neighboring symbols differ by more than one bit e.g. in 16-QAM, a symbol that represents a binary word 1101 is surrounded by four symbols representing 0101, 1100, 1001 and 1111. So if a symbol error is made, only one bit would be in error. However, one must note that this is true only in good signal conditions. When the SNR is low (noise has a higher magnitude) the symbol might be displaced to a location that is not adjacent and we might get higher number of bits in error.
Hard Decision
The concept of hard decision decoding is important when talking about channel coding, which we have not used in the above simulation. However, we will briefly explain it here. Hard decision is based on what is called “Hamming Distance” whereas soft decision is based on what it called “Euclidean Distance”. Hamming Distance is the distance of a code word in binary form, such as 011 differs from 010 and 001 by 1. Whereas the Euclidean distance is the distance before a decision is made that a bit is zero or one. So if the received sequence is 0.1 0.6 0.7 we get a Euclidean distance of 0.8124 from 010 and 0.6782 from 001. So we cannot make a hard decision about which sequence was transmitted based on the received sequence of 011. But based on the soft metrics we can make a decision that 001 was the most likely sequence that was transmitted (assuming that 010 and 001 were the only possible transmitted sequences).