The Fourier Transform is often used in Communication and Signal Processing to find the spectral content of a time-domain signal. The most common example is that of a sinusoid in the time domain, resulting in a sharply peaked signal in the frequency domain, also known as a delta function. A rectangular pulse in the time domain has a more complicated frequency domain equivalent, a sinc function. A rectangular pulse may be thought of as a combination of many sinusoids, hence its frequency domain equivalent is not that straightforward.

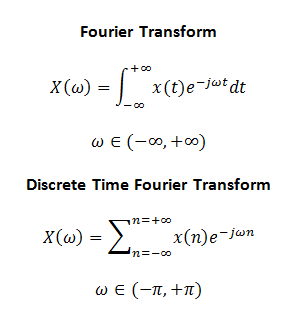
Now we would like to address a fundamental question: Why does Fourier Transform work the way it does? How does the multiplication of the time domain signal with a rotating exponential inside an integral result in such amazing insights about the signal? The answer is simple, think you are running in the park with a friend. You are wearing a smartwatch, while he is not. He asks you what his speed is. You slightly adjust your speed to come to par with your friend and then read the speed the smartwatch shows. Since you two are now running at the same speed, your smartwatch tells his speed as well.

Another example is when you are traveling in a car and a train track runs parallel to the highway. Now you want to measure the speed of a passing train while driving your car on the highway. You step on the gas until the speed of the car reaches the speed of the train and then just look up the speed on the speed gauge of your car. The Fourier Transform performs the same function. It searches for the rotating exponential that has the same speed as that of the rotating signal. The integral just performs summation or loosely speaking it performs averaging to smoothen out the results. 

The above has been explained for a complex signal but surprisingly it works for real signals as well.          

Note:

1. When the speed of two rotating exponentials is not the same, the multiplication operation followed by the integration operation would result in the cancellation of unmatched vectors. 
2. Integration operation is replaced by summation in Discrete Time Fourier Transform (DTFT).
3. The frequency resolution of the Fourier Transform depends upon the length of the temporal window. If the window size is T secs, Fourier Transform will have a frequency resolution of 1/T Hz.
4. The frequency resolution of the Fourier Transform has nothing to do with the sampling frequency (with T fixed).
5. A practical implementation of the Fourier Transform is known as the Fast Fourier Transform (FFT) and is widely used in academia and industry. 
6. A parting thought. What will happen if the speed of the train in the above example is continuously varying? 

Author: Yasir Ahmed (aka John)

More than 20 years of experience in various organizations in Pakistan, the USA, and Europe. Worked as a Research Assistant within the Mobile and Portable Radio Group (MPRG) of Virginia Tech and was one of the first researchers to propose Space Time Block Codes for eight transmit antennas. The collaboration with MPRG continued even after graduating with an MSEE degree and has resulted in 12 research publications and a book on Wireless Communications. Worked for Qualcomm USA as an Engineer with the key role of performance and conformance testing of UMTS modems. Qualcomm is the inventor of CDMA technology and owns patents critical to the 4G and 5G standards.

Twitter Facebook Linkedin