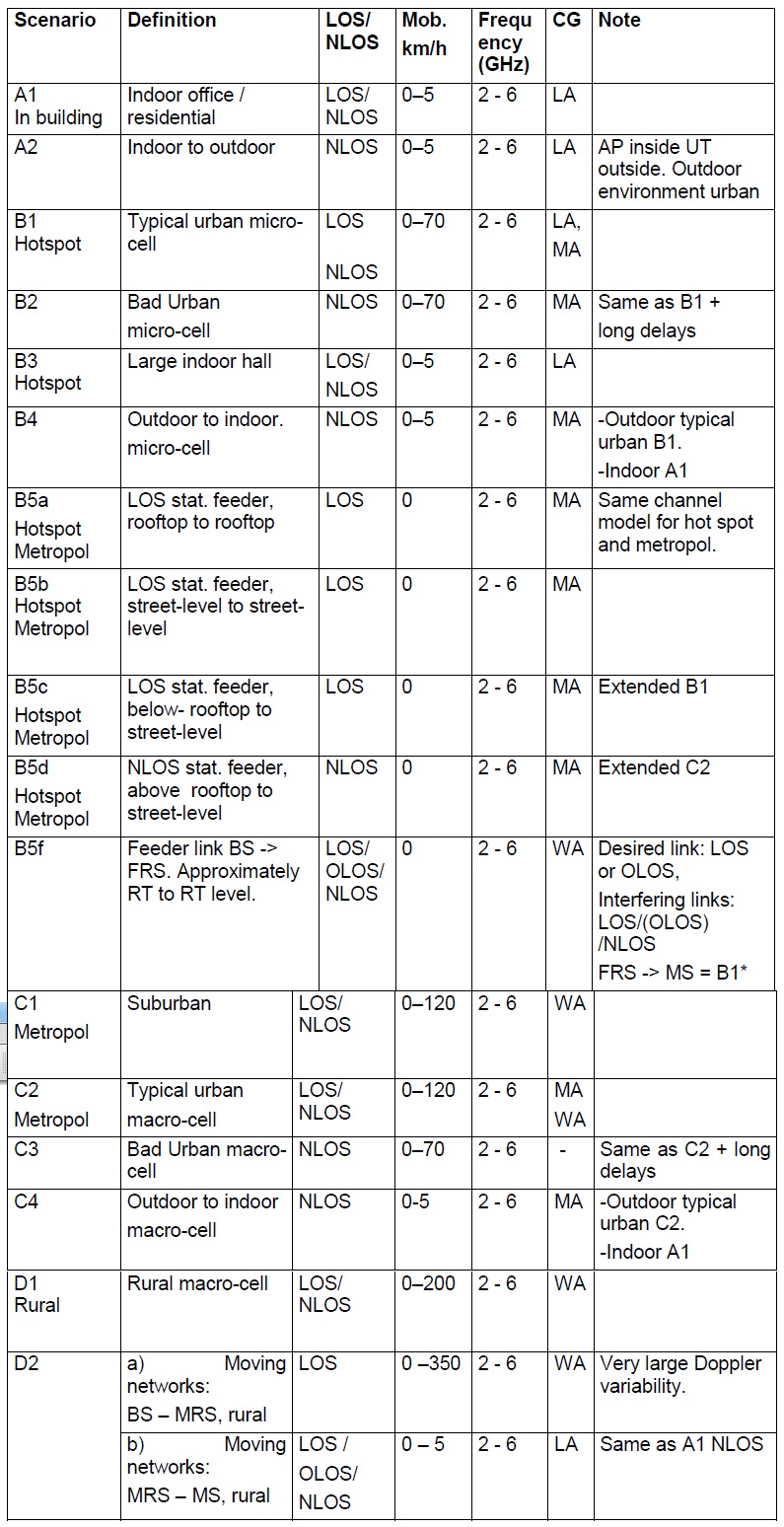
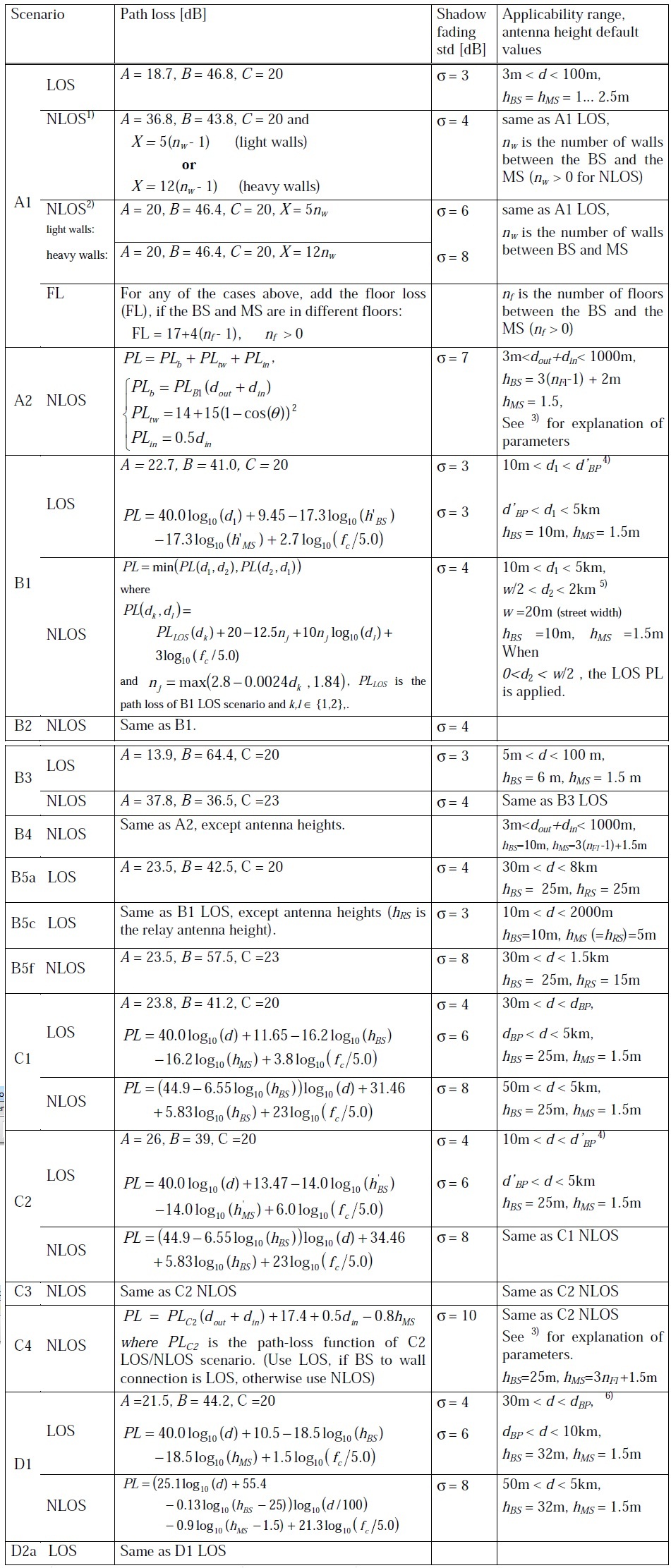
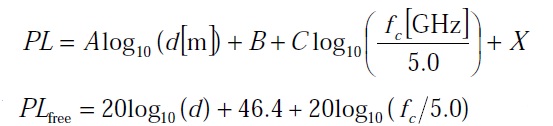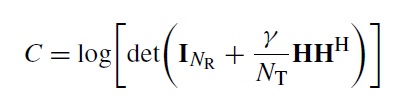Tag Archives: Channel

Sum of Sinusoids Fading Simulator

Channel Modeling, , , ,

We have previously looked at frequency domain fading simulators i.e. simulators that define the Doppler components in the frequency domain and then perform an IDFT to get the time domain signal. These simulators include Smith’s Simulator, Young’s Simulator and our very own Computationally Efficient Rayleigh Fading Simulator. Another technique that has been widely reported in the literature is Sum of Sinusoids Method. As the name suggests this method generates the Doppler components in the time domain and then sums them up to generate the time domain fading envelope. There are three parameters that define the properties of the generated signal.

1) Number of sinusoids – Higher the number better the properties of the generated signal but greater the computational complexity
2) Angle of arrival – This can be generated statistically or deterministically, spread from –pi to pi.
3) Phase of the arriving wave – This is uniformly distributed between –pi and pi.

The MATLAB code below gives three similar sum of sinusoids techniques for generating a Rayleigh faded envelope [1].

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% SUM OF SINUSOIDS FADING SIMULATORS
% fd - Doppler frequency  
% fs - Sampling frequency
% ts - Sampling period
% N - Number of sinusoids
%
% www.raymaps.com
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

clear all
close all

fd=70;
fs=1000000;
ts=1/fs;
t=0:ts:1;
N=100;

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Method 1 - Clarke
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
x=zeros(1,length(t));
y=zeros(1,length(t));

for n=1:N;n
    alpha=(rand-0.5)*2*pi;
    phi=(rand-0.5)*2*pi;
    x=x+randn*cos(2*pi*fd*t*cos(alpha)+phi);
    y=y+randn*sin(2*pi*fd*t*cos(alpha)+phi);
end
z=(1/sqrt(N))*(x+1i*y);
r1=abs(z);

plot(t,10*log10(r1))
hold on

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Method 2 - Pop, Beaulieu
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
x=zeros(1,length(t));
y=zeros(1,length(t));

for n=1:N;n
    alpha=2*pi*n/N;
    phi=(rand-0.5)*2*pi;
    x=x+randn*cos(2*pi*fd*t*cos(alpha)+phi);
    y=y+randn*sin(2*pi*fd*t*cos(alpha)+phi);
end
z=(1/sqrt(N))*(x+1i*y);
r2=abs(z);

plot(t,10*log10(r2),'r')
hold on

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Method 3 - Chengshan Xiao
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
x=zeros(1,length(t));
y=zeros(1,length(t));

for n=1:N;n
    phi=(rand-0.5)*2*pi;
    theta=(rand-0.5)*2*pi;
    alpha=(2*pi*n+theta)/N;
    x=x+randn*cos(2*pi*fd*t*cos(alpha)+phi);
    y=y+randn*sin(2*pi*fd*t*cos(alpha)+phi);
end
z=(1/sqrt(N))*(x+1i*y);
r3=abs(z);

plot(t,10*log10(r3),'g')
hold off

xlabel('Time(sec)')
ylabel('Envelope(dB)')
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

All the three techniques given above are quite accurate in generating a Rayleigh faded envelope with the desired statistical properties. The accuracy of these techniques increases as the number of sinusoids goes to infinity (we have tested these techniques with up to 1000 sinusoids but realistically speaking even 100 sinusoids are enough). If we want to compare the three techniques in terms of the Level Crossing Rate (LCR) and Average Fade Duration (AFD) we can say that the first and third technique are a bit more accurate than the second technique. Therefore we can conclude that a statistically distributed angle of arrival is a better choice than a deterministically distributed angle of arrival. Also, if we look at the autocorrelation of the in-phase and quadrature components we see that for the first and third case we get a zero order Bessel function of the first kind whereas for the second case we get a somewhat different sequence which approximates the Bessel function with increasing accuracy as the number of sinusoids is increased.

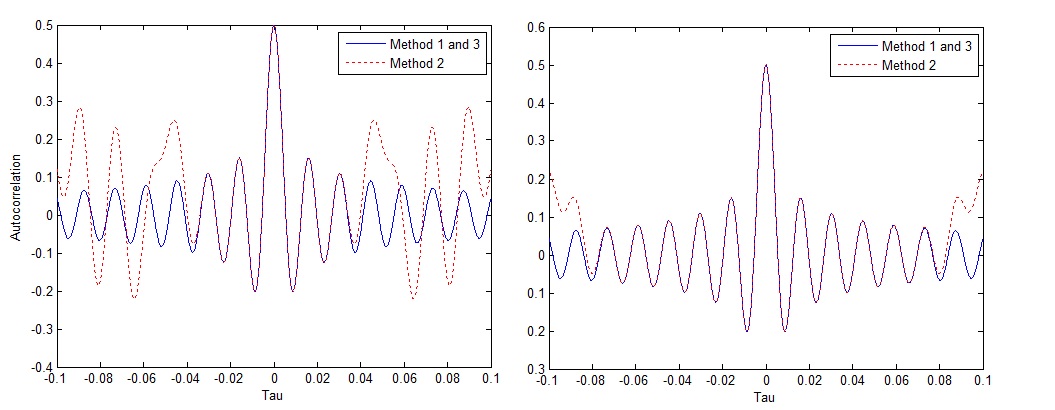
Correlation of Real and Imaginary Parts
Correlation of Real and Imaginary Parts

The above figures show the theoretical Bessel function versus the autocorrelation of the real/imaginary part  generated by method number two. The figure on the left considers 20 sinusoids whereas the figure on the right considers 40 sinusoids. As can be seen the accuracy of the autocorrelation sequence increases considerably by doubling the number of sinusoids. We can assume that for number of sinusoids exceeding 100 i.e. N=100 in the above code the generated autocorrelation sequence would be quite accurate.

[1] Chengshan Xiao, “Novel Sum-of-Sinusoids Simulation Models for Rayleigh and Rician Fading Channels,” IEEE TRANSACTIONS ON WIRELESS COMMUNICATIONS, VOL. 5, NO. 12, DECEMBER 2006.

Uniform, Gaussian and Rayleigh Distribution

Channel Modeling, Fundamentals, , ,

It is sometimes important to know the relationship between various distributions. This can be useful if there is a function available for one distribution and it can be used to derive other distributions. In the context of Wireless Communications it is important to know the relationship between the Uniform, Gaussian and Rayleigh distribution.

According to Central Limit Theorem the sum of a large number of independent and identically distributed random variables has a Gaussian distribution. This is used to model the amplitude of the in-phase and quadrature components of a wireless signal. Shown below is the model for the received signal which has been modulated by the Gaussian channel coefficients g1 and g2.

r=g1*a1*cos(2*pi*fc*t)+g2*a2*sin(2*pi*fc*t)

The envelope of this signal (sqrt(g1^2+g2^2)) as a Rayleigh distribution. Now if you only had a function for Uniform Distribution you can generate Rayleigh Distribution using the following routine.

clear all
close all
M=10000;
N=100;

for n=1:M;
x1=rand(1,N)-0.5;
x2=rand(1,N)-0.5;

y1=mean(x1);
y2=mean(x2);

z(n)=sqrt(y1^2+y2^2);
end

hist(z,20)

Note: Here a1 and a2 can be considered constants (at least during the symbol duration) and its really g1 and g2 that are varying.

Fading Model – From Simple to Complex

Fundamentals, , ,

1. The simplest channel model just scales the input signal by a real number between 0 and 1 e.g. if the signal at the transmitter is s(t) then at the receiver it becomes a*s(t). The effect of channel is multiplicative (the receiver noise on the other hand is additive).

2.   The above channel model ignores the phase shift introduced by the channel. A more realistic channel model is one that scales the input signal as well rotates it by a certain angle e.g. if s(t) is the transmitted signal then the received signal becomes a*exp(jθ)*s(t).

3. In a realistic channel the transmitter, receiver and/or the environment is in motion therefore the scaling factor and phase shift are a function of time e.g. if s(t) is the transmitted signal then the received signal is a(t)*exp(jθ(t))*s(t). Typically in simulation of wireless communication systems a(t) has a Rayleigh distribution and θ(t) has a uniform distribution.

4. Although the above model is quite popular, it can be further improved by introducing temporal correlation in the fading envelope. This can be achieved by the Smith’s simulator which uses a frequency domain approach to characterize the channel. The behavior of the channel is controlled by the Doppler frequency fd. Higher the Doppler frequency greater is the variation in the channel and vice versa [1].

5. Finally the most advanced wireless channel model is one that considers the channel to be an FIR filter where each tap is defined by the process outlined in (4). The channel thus performs convolution on the signal that passes through it. In the context of LTE there are three channel models that are defined namely Extended Pedestrian A (EPA), Extended Vehicular A (EVA) and Extended Typical Urban (UTU) [2].

Note: As an after thought I have realized that this channel model becomes even more complicated with the introduction of spatial correlation between the antennas of a MIMO system [3].

Implementing a Non-Uniformly Spaced Tapped Delay Line Channel Model

Channel Modeling, LTE, , ,

Question:
Since you are good on fundamentals I would like to ask you a question that puzzles me. LTE channels models are defined at irregular time intervals as shown in [1].

The EPA, EVA and ETU channel taps can best be described as being sampled at multiples of 10 nsec. However, LTE signal is sampled at multiples of 3.84 MHz (Ts=260.416667 nsec). So how does one perform convolution operation.

Answer:
Empirical multipath channel is usually characterized as a τ-spaced tapped delay line (TDL), whose power delay profile (PDP) is either uniformly spaced, or more frequently, spaced with arbitrary time delay(s). Converting a τ-spaced empirical model to a more tractable T-spaced (sampling time-spaced) statistical model will greatly facilitate the link-level simulation and performance evaluation of the broadband digital wireless system. The practical approaches to accomplish this task could be either approximation or interpolation,

1. Approximation
a. Ceil or Floor a τ-spaced tap to the neighbouring sampling time.
b. Split the energy of a τ-spaced tap to the adjacent sampling times.
2. Interpolation
An Ideal Bandlimited (sinc) Interpolator can fulfil the goal.

It should be noted that although T-spaced statistical model is simpler for analysis, τ-spaced empirical model represents the channel more accurately.

[1] http://www.steepestascent.com/content/mediaassets/html/LTE/Help/PropagationConditions.html

WINNER-II Path Loss Model

Channel Modeling, LTE, , , , ,

In simple terms the path loss is the difference between the transmitted power and the received power of a wireless communication system. This may range from tens of dB to more than a 100 dB e.g. if the transmitted power of a wireless communication system is 30 dBm and the received power is -90 dBm then the path loss is calculated as 30-(-90)=120 dB. Path loss is sometimes categorized as a large scale effect (in contrast to fading which is a small scale effect).

According to the WINNER-II model the path loss can be calculated  as:

WINNER-II Path Loss Equation
WINNER-II Path Loss Equation

Here d is the separation between the transmitter and receiver in meters, fc is the frequency in GHz, A is the path loss exponent, B is the intercept and C is the frequency dependent parameter. X is the environment specific parameter such as path loss due to a wall. PLfree is the path loss in a free space line of sight environment (here A=20, B=46.4 and C=20).

The table below describes the different environments defined in the WINNER-II model. Once an environment is selected the path loss parameters A, B and C can be selected from the table further down e.g. A1 is the in-building scenario with A=18.7, B=46.8 and C=20 for the LOS case. The PL for a T-R separation of 100 m and frequency of 2 GHz is calculated as:

PL=18.7*log10(100)+46.8+20*log10(2/5)=76.42 dB

A separate equation for the path loss is given where the parameters A, B and C are not sufficient to describe the scenario.

WINNER-II Propagation Scenarios
WINNER-II Propagation Scenarios
WINNER-II Path Loss Models
WINNER-II Path Loss Models

Note:

1. Here CG is the concept group that developed the particular scenario. This is either Local Area (LA), Metropolitan Area (MA) or Wide Area (WA).

2. For more details visit:

L. Hentilä, P. Kyösti, M. Käske, M. Narandzic , and M. Alatossava. (2007, December.) MATLAB implementation of the WINNER Phase II Channel Model ver1.1 [Online]. Available: https://www.ist-winner.org/phase_2_model.html

 

MIMO Capacity in a Fading Environment

Capacity, LTE, WiMAX, , , , , , , , ,

The Shannon Capacity of a channel is the data rate that can be achieved over a given bandwidth (BW) and at a particular signal to noise ratio (SNR) with diminishing bit error rate (BER). This has been discussed in an earlier post for the case of SISO channel and additive white Gaussian noise (AWGN). For a MIMO fading channel the capacity with channel not known to the transmitter is given as (both sides have been normalized by the bandwidth [1]):

Shannon Capacity of a MIMO Channel
Shannon Capacity of a MIMO Channel

where NT is the number of transmit antennas, NR is the number of receive antennas, γ is the signal to interference plus noise ratio (SINR), INR is the NRxNR identity matrix and H is the NRxNT channel matrix. Furthermore, hij, an element of the matrix H defines the complex channel coefficient between the ith receive antenna and jth transmit antenna. It is quite obvious that the channel capacity (in bits/sec/Hz) is highly dependent on the structure of matrix H. Let us explore the effect of H on the channel capacity.

Let us first consider a 4×4 case (NT=4, NR=4) where the channel is a simple AWGN channel and there is no fading. For this case hij=1 for all values of i and j. It is found that channel capacity of this simple channel for an SINR of 10 dB is 5.36bits/sec/Hz. It is further observed that the channel capacity does not change with number of transmit antennas and increases logarithmically with increase in number of receive antennas. Thus it can be concluded that in an AWGN channel no multiplexing gain is obtained by increasing the number of transmit antennas.

We next consider a more realistic scenario where the channel coefficients hij are complex with real and imaginary parts having a Gaussian distribution with zero mean and variance 0.5. Since the channel H is random the capacity is also a random variable with a certain distribution. An important metric to quantify the capacity of such a channel is the Complimentary Cumulative Distribution Function (CCDF). This curve basically gives the probability that the MIMO capacity is above a certain threshold.

Complimentary Cumulative Distribution Function of Capacity
Complimentary Cumulative Distribution Function of Capacity

It is obvious (see figure above) that there is a very high probability that the capacity obtained for the MIMO channel is significantly higher than that obtained for an AWGN channel e.g. for an SINR of 9 dB there is 90% probability that the capacity is greater than 8 bps/Hz. Similarly for an SINR of 12 dB there is a 90% probability that the capacity is greater than 11 bps/Hz. For a stricter threshold of 99% the above capacities are reduced to 7.2 bps/Hz and 9.6 bps/Hz.

In a practical system the channel coefficients hij would have some correlation which would depend upon the antenna spacing. Lower the antenna spacing higher would be the antenna correlation and lower would be the MIMO system capacity. This would be discussed in a future post.

The MATLAB code for calculating the CCDF of channel capacity of a MIMO channel is given below.

clear all
close all

Nr=4;
Nt=4;
I=eye(Nr);
g=15.8489;

for n=1:10000
    H=sqrt(1/2)*randn(Nr,Nt)+j*sqrt(1/2)*randn(Nr,Nt);
    C(n)=log2(det(I+(g/Nt)*(H*H')));
end

[a,b]=hist(real(C),100);
a=a/sum(a);
plot(b,1-cumsum(a));
xlabel('Capacity (bps/Hz)')
ylabel('Probability (Capacity > Abcissa)')
grid on

[1] G. J. Foschini and M. J. Gans,”On limits of Wireless Communications in a Fading Environment when Using Multiple Antennas”, Wireless Personal Communications 6, pp 311-335, 1998.