Quadrature Amplitude Modulation (QAM) is an important modulation scheme as it allows for higher data rates and spectral efficiencies. The bit error rate (BER) of QAM can be calculated through Monte Carlo simulations. However this becomes quite complex as the constellation size of the modulation schemes increases. Therefore a theoretical approach is sometimes preferred. The BER for Gray coded QAM, for even number of bits per symbol, is shown below.
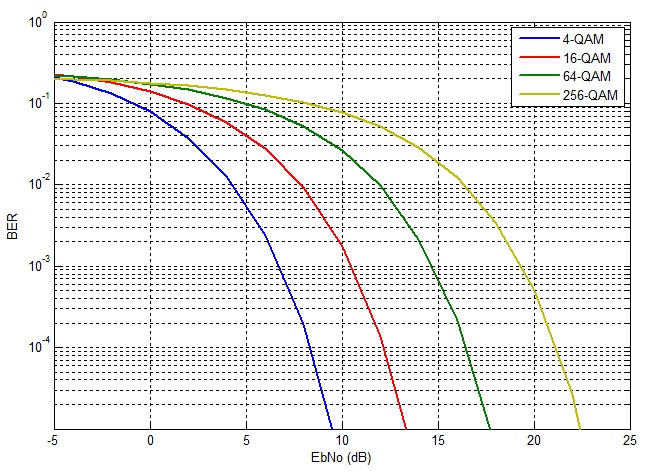
Gray coding ensures that a symbol error results in a single bit error. The code for calculating the theoretical QAM BER for k even (even number of bits per symbol) is given below. The formula for calculating the BER for k odd is different, however, the formula given below can be used a first estimate.
EbNodB=-6:2:24
EbNo=10.^(EbNodB/10);
k=8;
M=2^k;
x=sqrt(3*k*EbNo/(M-1));
Pb=(4/k)*(1-1/sqrt(M))*(1/2)*erfc(x/sqrt(2));
semilogy(EbNodB,Pb)
Note:
1. Each additional bit/symbol requires about 2dB extra in SNR to achieve the same BER.
2. 4-QAM is essentially QPSK modulation.
Author: Yasir
More than 20 years of experience in various organizations in Pakistan, the USA, and Europe. Worked with the Mobile and Portable Radio Group (MPRG) of Virginia Tech and Qualcomm USA and was one of the first researchers to propose Space Time Block Codes for eight transmit antennas. Have publsihed a book “Recipes for Communication and Signal Processing” through Springer Nature.
41 thoughts on “QAM Theoretical BER in AWGN”
can you share the code for the theoretical BER of 64QAM in AWGN versus SNR(dB) instead of Eb/No(dB)?
Thank you
Hi,
Can you please provide the bit error rate of 16-QAM modulation through MATLAB simulations using oversampling.
Thank you in advance
Hi Rahul,
There are two ways you can approach this problem (each requiring a bit of work from you).
– You can modify the code for 64-QAM by just changing the parameter M from 64 to 16 and run the BER simulation.
http://www.raymaps.com/index.php/ber-64-qam-awgn/
– If you want to go back to basics you can use the 4-PAM code for this. 16-QAM is nothing but two orthogonal 4-PAM constellations.
http://www.raymaps.com/index.php/pulse-amplitude-modulation-symbol-error-rate-in-awgn/
I hope this was helpful!
Thank you John for the reply. I tried to build the same from your this post
http://www.raymaps.com/index.php/m-qam-bit-error-rate-in-rayleigh-fading/
But when I using the oversampling factor, I am not able to normalize it properly. Can you please look at the below code and suggest any recommended changes. Thank you.
clc
clear all
close all
N = 10000; % Number of bits
Oversamp =8; % oversamling factor
itr=5;
M=16;
k=log2(M);
EbNodB = 0:2:10;
for ii = 1:length(EbNodB)
nErr =[];
for kk = 1:itr
%% Transmitter
x=transpose(round(rand(1,N)));
h1=modem.qammod(M);
h1.inputtype=’bit’;
h1.symbolorder=’gray’;
y=modulate(h1,x);
y1 = transpose(y);
Sig = ones(Oversamp,1)*y1;
Sig1 = (1/sqrt(Oversamp))*(Sig(:));
%% Channel
EbNo=10.^(EbNodB(ii)/10);
Eb=mean((abs(Sig1)).^2)/k;
sigma=sqrt(Eb/(2*EbNo));
w=sigma*(randn(Oversamp*N/k,1)+1i*randn(Oversamp*N/k,1));
rx= Sig1 + w;
%% Receiver
rr = transpose(rx);
Rx_sig = reshape(rr,Oversamp,N/k);
Rx_sig1 = ones(1,Oversamp)*Rx_sig;
r = transpose(Rx_sig1);
h2=modem.qamdemod(M);
h2.outputtype=’bit’;
h2.symbolorder=’gray’;
h2.decisiontype=’hard decision’;
z=demodulate(h2,r);
count=(N-sum(x==z))/N ;
nErr = [nErr count];
end
Err(ii) = sum(nErr)/itr;
end
simBer = Err; % simulated ber
EbNo=10.^(EbNodB/10);
x=sqrt(3*k*EbNo/(M-1));
theoryBerAWGN=(4/k)*(1-1/sqrt(M))*(1/2)*erfc(x/sqrt(2));
semilogy(EbNodB,theoryBerAWGN,’bd-‘,’LineWidth’,2);
hold on
semilogy(EbNodB,simBer,’rx-‘,’LineWidth’,2);
hold on
legend(‘AWGN-Theory’, ‘Simulation’);
xlabel(‘Eb/No, dB’);
ylabel(‘Bit Error Rate’)
I think there is a problem with this line:
Eb=mean((abs(Sig1)).^2)/k;
It should be:
Eb=Oversamp*mean((abs(Sig1)).^2)/k;
Thank you for your reply.
But still, it doesn’t work.
Thank you so much John. Now code is working fine.
For the normalization, we divide by sqrt(Oversamp), both at the transmitter and receiver.
And also after oversampling bit energy equals Eb=Oversamp*mean((abs(Sig1)).^2)/k;
The complete code is given below:
%% Transmitter
x=transpose(round(rand(1,N)));
h1=modem.qammod(M);
h1.inputtype=’bit’;
h1.symbolorder=’gray’;
y=modulate(h1,x);
y1 = transpose(y);
Sig = ones(Oversamp,1)*y1;
Sig1 = (1/sqrt(Oversamp))*(Sig(:));
%% Channel
EbNo=10.^(EbNodB(ii)/10);
% Eb=mean((abs(Sig1)).^2)/k;
Eb=Oversamp*mean((abs(Sig1)).^2)/k;
sigma=sqrt(Eb/(2*EbNo));
w=sigma*(randn(Oversamp*N/k,1)+1i*randn(Oversamp*N/k,1));
rx= Sig1 + w;
%% Receiver
rr = transpose(rx);
Rx_sig = reshape(rr,Oversamp,N/k);
Rx_sig1 = (1/sqrt(Oversamp))*ones(1,Oversamp)*Rx_sig;
r = transpose(Rx_sig1);
h2=modem.qamdemod(M);
h2.outputtype=’bit’;
h2.symbolorder=’gray’;
h2.decisiontype=’hard decision’;
z=demodulate(h2,r);
count=(N-sum(x==z))/N ;
hello,
i tried to integrate qpsk and 16qam with turbo code. I am not able to obtain the right result. Can someone help me?
thank you very much.
I have not discussed turbo codes so far…but maybe some day I will do…
Hello all, can someone help me with this problem?
In a QPSK system, the channel has a combination of AWGN n[k] and interference I[k] which is also AWGN. The average transmit power is Pt, the noise spectral density is 10^(−8) W/Hz, the channel bandwidth B is 10 KHz (receiver noise power is N0B), and the interference power is Pi.
Question: Please simulate the average Symbol Error Rate vs SINR (signal-to-noise-plus-interference ratio) in Matlab. Please derive the average SER and plot the theoretical average SER vs SINR in the same figure.
Dayn, you need to understand the following to do this assignment:
Noise or Interference Power: Bandwidth x Noise or Interference PSD
Total Noise and Interference Power: Noise Power + Interference Power
Signal to Interference and Noise Ratio (SINR): Signal Power / (Noise Power + Interference Power)
Since this is an assignment I would like to leave the rest to you. Plus you can take the help from the blog (be careful not to mix up SNR, SINR and EbNo).
Consider the following interference channel
The channel has a combination of AWGN n[k] and interference I[k]. We model I[k] as AWGN. The average transmit power is Pt, the noise spectral density is 10^(−8) W/Hz, the channel bandwidth B is 10 KHz (receiver noise power is NoB), and the interference power is Pi.
1. Please simulate the average SER vs SINR in Matlab. Please derive the average SER and plot the theoretical average SER vs SINR in the same figure.
2. Assume that the interferer is on (i.e. the switch is down) with probability 0.25 and off (i.e. the switch is up) with probability 0.75. Pt=10 mW, and Pi =9 mW.
Please do the following.
2.1 What is the Shannon capacity of the channel if neither transmitter nor receiver know when the interferer is on?
2.2 What is the capacity of the channel if both transmitter and receiver know when the interferer is on?
2.3 Suppose now that the interferer is a malicious jammer with perfect knowledge of x[k] (so the interferer is no longer modeled as AWGN). Assume that neither transmitter nor receiver have knowledge of the jammer behavior. Assume also that the jammer is always on
and has an average transmit power of 10 mW. What strategy should the jammer use to minimize the SNR of the received signal?
3 What insight can you get from the above exercise?
Pt=10mWatt
Pi=9mWatt
Pn=10^(-8)*10000=0.1mWatt
P_ON=0.25
P_OFF=0.75
In case it is known when the jammer is on and when its off the capacity would be sum of two capacities.
C_ON=B*log2(1+SINR)=10000*log2(1+10/(0.1+9))=10000*log2(2.0989)=10696 bits/sec
C_OFF=B*log2(1+SNR)=10000*log2(1+10/0.1)=10000*log2(101)=66582 bits/sec
C_Total=P_ON*C_ON+P_OFF*C_OFF=0.25*10696+0.75*66582=52610 bits/sec
If it is not known when the jammer is on you can adopt one of two strategies.
1. Always transmit at the lower rate dictated by presence of jammmer.
2. Always transmit at the higher rate and totally lose the signal for 25% of the time.
Figure out which one is better!
Revisiting this post after a long time I thought I might give a go to the case I briefly mentioned in the end, with the two strategies:
Strategy 1: 10696 bits/sec
Strategy 2: 0.75*66582=49936 bits/sec
Obviously Strategy 2 is better as you can send a lot more bits when the jammer is off (75% of the time).
Best way to reduce the power of the signal is to transmit a jamming signal which is equal in power to the transmitted signal but phase reversed. Not an easy thing to do but theoretically the best option.
How are you doing
I am doing the performance analysis of quasi-orthogonal space-time codes under QAM debugging, using MATLAB simulation, but I do not know the error rate simulation formula How to say, is the same as you write the simulation formula? If not, do you know what it is? I have a piece of code but is under QPSK debugging, its simulation formula is PPQOSTBC (KK) = 0.5*ERFC (sqrt (0.5*SNRQOSTBC)). Can you tell me if you know?
Thank you so much
Please look at the post on Alamouti codes to get a basic understanding.
http://www.raymaps.com/index.php/alamouti-scheme/
I simulate the BER performance of M-ary QAM .
now I want to check that result with theoretical ber. So, please send to me theoretical BER equation of M-ary QAM
thank U
Its already given. Please go through the above post carefully.
Hello, Can someone please help me with the following?
The source generates equal probable symbols, P(si) = 0.125, i=0,…,7, and Gray mapping is used to map information bits to the PAM signals.
(a) Create a Matlab program so it can simulate the symbol error performance and the
bit error rate performance of the 8-PAM communication system for the transmission of packets of 10,000 symbols each.
(b) Using your program to simulate the symbol error performance and the bit error
performance of the system with
Eb/N0 = 0, 2, 4, 6, 8, 10 dB.
So far, I have the following code.
N = 10^4; % number of symbols
>> alpha8pam = [-7 -5 -3 -1 1 3 5 7]; % 8-PAM alphabets
>> Es_N0_dB = [0:2:4:6:8:10]; % multiple Eb/N0 values
>> ipHat = zeros(1,N);
for ii = 1:length(Es_N0_dB)
ip = randsrc(1,N,alpha8pam);
s = (1/sqrt(5))*ip; % normalization of energy to 1
n = 1/sqrt(2)*[randn(1,N) + j*randn(1,N)]; % white guassian noise, 0dB variance
y = s + 10^(-Es_N0_dB(ii)/20)*n; % additive white gaussian noise
% demodulation
r = real(y); % taking only the real part
ipHat(find(r= 2/sqrt(5))) = 3;
ipHat(find(r>=-2/sqrt(5) & r=0 & r<2/sqrt(5))) = 1;
I'm not sure how to write the rest of the 'iphat' values.
Please look at the following post:
https://www.raymaps.com/index.php/pulse-amplitude-modulation-symbol-error-rate-in-awgn/
Sir can you tell me the formula theoretical BER of Tilted Quadrature Amplitude Modulation for rayleigh
Please see if the following post is useful.
https://www.raymaps.com/index.php/m-qam-bit-error-rate-in-rayleigh-fading/
Hello,
Can you please give us the theoretical Symbol Error Rate of a PAM Modulation?
Thank you!
Some valuable information about PAM can be found here:
http://www.mathworks.com/help/comm/ug/bit-error-rate-ber.html#bq423z2
John
Please look at the following post:
https://www.raymaps.com/index.php/pulse-amplitude-modulation-symbol-error-rate-in-awgn/
My Octave version.
I’m new to Octave and doing this sort of thing so please offer suggestions and corrections.
function Y=Q(X)
Y=0.5.*erfc(double(X)./sqrt(2))
endfunction
EbNodB=0:2:30
EbNo=10.^(EbNodB/10)
K=[2 4 6 8]
M=2.^K
KM=double(3*K./(M-1))
KME=double(KM’*EbNo)
X=double(sqrt(KME))
Pb=double((4./K).*(1-1./sqrt(M)))’.*Q(X)
semilogy(EbNodB,Pb)
title(“M-QAM BER v SNR”)
grid on
grid minor on
legend(num2str(M’))
ylim([1e-8 1e0])
xlabel(“Eb/No (dB)”)
ylabel(“BER”)
print -dsvg q.svg
I love using Octave too. Keep up the good work!
Hello,
I am not able to reproduce that graphic, could you send me the complete matlab code?
Thank you!
This is the complete code. You should be able to reproduce the above Fig. If you are still unable to do so, please share your code here.
John
I simulate the BER performance of M-ary QAM over Rayleigh fading channel in Matlab tool, now I want to check that result with theoretical ber. So, please send to me theoretical BER equation of M-ary QAM over Rayleigh fading channel.
Thanking you.
Please see if the following post is useful.
https://www.raymaps.com/index.php/m-qam-bit-error-rate-in-rayleigh-fading/
Hello, it seems that everyone is in need of those codes :). Could you send me the code for matlab also??
I’ll appreciate it. Thank you!!
plz send me BER 64 QAM modulation code in AWGN
I´ve proved with the same code and the result was diferent
Gordon: Frankly speaking I could not figure this out easily and had to do a simulation. It turns out that there is significant difference (2-3 dB) at low EbNo but at higher signal to noise ratios the difference is reduced to a fraction of a dB.
The simulation considered 64-QAM modulation but similar results are expected for other modulation schemes.
May I know the sensitivity difference between the cases with and without gray coding?
Best
Gordon
Hello,
I tried to do the graphic that you upload to the website in order to calculate the theorical BER of 4-QAM, 16-QAM and 64-QAM.
I am not able to reproduce that graphic, could you send me the complete matlab code??
Thank you very much
Just use the code as it is. Change ‘k’ to get the different curves (k=2,4,6,8).
What if k is odd
K=3 for 8QAM
The same formula can be used for k odd, its reasonably accurate. If it does not work let me know.