Shannon Capacity of LTE in AWGN can be calculated by using the Shannon Capacity formula:
C=B*log2(1+SNR)
or
C=B*log2(1+P/(B*No))
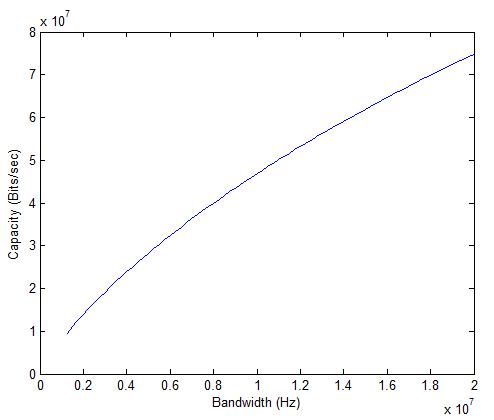
The signal power P is set at -90dBm, the Noise Power Spectral Density No is set at 4.04e-21 W/Hz (-174dBm/Hz) and the bandwidth is varied from 1.25MHz to 20MHz.
It is seen that the capacity increases from about 10Mbps to above 70Mbps as the bandwidth is varied from 1.25MHz to 20MHz (keeping the signal power constant). It must be noted that this is the capacity with a single transmit and single receive antenna (MIMO capacity would obviously be higher).
Author: Yasir Ahmed (aka John)
More than 20 years of experience in various organizations in Pakistan, the USA, and Europe. Worked as a Research Assistant within the Mobile and Portable Radio Group (MPRG) of Virginia Tech and was one of the first researchers to propose Space Time Block Codes for eight transmit antennas. The collaboration with MPRG continued even after graduating with an MSEE degree and has resulted in 12 research publications and a book on Wireless Communications. Worked for Qualcomm USA as an Engineer with the key role of performance and conformance testing of UMTS modems. Qualcomm is the inventor of CDMA technology and owns patents critical to the 4G and 5G standards.
Which modulation is considered here to get 70Mbps for 20MHz B? For 16QAM then 67Mbps or nearly 70 Mbps is correct but with 64QAM it is 100Mbps. Assuming SISO. Else I am not understanding how you came across 70Mbps for 20 MHz (same goes for 1.25MHz).
Thanks
This is the theoretical maximum given a certain Signal to Noise Ratio (SNR). If you keep increasing the SNR you will get higher theoretical capacities. I would encourage you to experiment yourself with the formula.
How C for BW 20MHz is 70Mbps? For complete 20 MHz it’s coming around 271Mbps. Thanks.
This is the theoretical maximum given a certain Signal to Noise Ratio (SNR). If you keep increasing the SNR you will get higher theoretical capacities. I would encourage you to experiment yourself with the formula.
So, channel capacity is relatively higher with narrow bandwidths.
Is this why LTE has lots of narrow resource blocks and sub-carriers?
Capacity does not change by dividing the frequency band into narrower frequency bins (keeping the SNR to be the same for each bin). Narrower frequency bins make the task of an equilizer easy since the frequency response over a frequency bin can be assumed to be constant.
Yes Satya you are right. I have made the correction. Thank you!
If I am not wrong, above plot is inbetween Capacity-Bandwidth rather than Capacity-SNR.
Kindly see to it.
Sir, Thanks
SNR = P/(B*No)
Keeping P and No constant, SNR or SNR(dB) will decrease with increase in B.
Of course, with increase in B, capacity increases giving capacity-bandwith plot correctly as plotted above.
But, capacity-SNR(dB) plot is coming otherwise. Since, in this case, capacity increases even if SNR(dB) decreases because of increased B.
http://www.raymaps.com/index.php/mimo-capacity-fading-environment/
Hi John,
Thanks for the post. Just a quick question, if Shannon’s Theorem was modelled in a Time-Invariant Channel using a channel realization matrix H with SNR = (P*|H|^2)/(noise variance), how will I obtain a capacity curve if I was to have fixed signal power P?
Currently I am varying P in order to obtain a curve similar to yours, with H being a random 1×1 (or 2×2) complex valued matrix.