The Shannon Capacity of a channel is the data rate that can be achieved over a given bandwidth (BW) and at a particular signal to noise ratio (SNR) with diminishing bit error rate (BER). This has been discussed in an earlier post for the case of SISO channel and additive white Gaussian noise (AWGN). For a MIMO fading channel the capacity with channel not known to the transmitter is given as (both sides have been normalized by the bandwidth [1]):
where NT is the number of transmit antennas, NR is the number of receive antennas, γ is the signal to interference plus noise ratio (SINR), INR is the NRxNR identity matrix and H is the NRxNT channel matrix. Furthermore, hij, an element of the matrix H defines the complex channel coefficient between the ith receive antenna and jth transmit antenna. It is quite obvious that the channel capacity (in bits/sec/Hz) is highly dependent on the structure of matrix H. Let us explore the effect of H on the channel capacity.
Let us first consider a 4×4 case (NT=4, NR=4) where the channel is a simple AWGN channel and there is no fading. For this case hij=1 for all values of i and j. It is found that channel capacity of this simple channel for an SINR of 10 dB is 5.36bits/sec/Hz. It is further observed that the channel capacity does not change with number of transmit antennas and increases logarithmically with increase in number of receive antennas. Thus it can be concluded that in an AWGN channel no multiplexing gain is obtained by increasing the number of transmit antennas.
We next consider a more realistic scenario where the channel coefficients hij are complex with real and imaginary parts having a Gaussian distribution with zero mean and variance 0.5. Since the channel H is random the capacity is also a random variable with a certain distribution. An important metric to quantify the capacity of such a channel is the Complimentary Cumulative Distribution Function (CCDF). This curve basically gives the probability that the MIMO capacity is above a certain threshold.
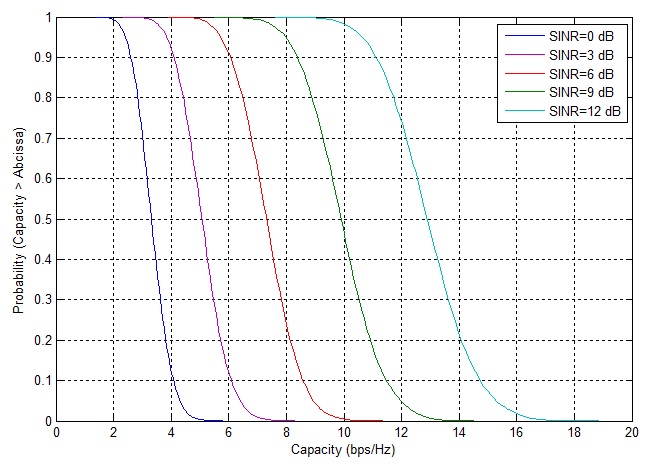
It is obvious (see figure above) that there is a very high probability that the capacity obtained for the MIMO channel is significantly higher than that obtained for an AWGN channel e.g. for an SINR of 9 dB there is 90% probability that the capacity is greater than 8 bps/Hz. Similarly for an SINR of 12 dB there is a 90% probability that the capacity is greater than 11 bps/Hz. For a stricter threshold of 99% the above capacities are reduced to 7.2 bps/Hz and 9.6 bps/Hz.
In a practical system the channel coefficients hij would have some correlation which would depend upon the antenna spacing. Lower the antenna spacing higher would be the antenna correlation and lower would be the MIMO system capacity. This would be discussed in a future post.
The MATLAB code for calculating the CCDF of channel capacity of a MIMO channel is given below.
clear all
close all
Nr=4;
Nt=4;
I=eye(Nr);
g=15.8489;
for n=1:10000
H=sqrt(1/2)*randn(Nr,Nt)+j*sqrt(1/2)*randn(Nr,Nt);
C(n)=log2(det(I+(g/Nt)*(H*H')));
end
[a,b]=hist(real(C),100);
a=a/sum(a);
plot(b,1-cumsum(a));
xlabel('Capacity (bps/Hz)')
ylabel('Probability (Capacity > Abcissa)')
grid on
[1] G. J. Foschini and M. J. Gans,”On limits of Wireless Communications in a Fading Environment when Using Multiple Antennas”, Wireless Personal Communications 6, pp 311-335, 1998.
Author: Yasir Ahmed (aka John)
More than 20 years of experience in various organizations in Pakistan, the USA, and Europe. Worked as a Research Assistant within the Mobile and Portable Radio Group (MPRG) of Virginia Tech and was one of the first researchers to propose Space Time Block Codes for eight transmit antennas. The collaboration with MPRG continued even after graduating with an MSEE degree and has resulted in 12 research publications and a book on Wireless Communications. Worked for Qualcomm USA as an Engineer with the key role of performance and conformance testing of UMTS modems. Qualcomm is the inventor of CDMA technology and owns patents critical to the 4G and 5G standards.
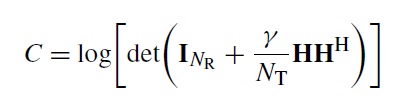
I’m really in need of a real simulation of Capacity of a system. I mean, here we just had a formula and wrote a one line matlab code to plot the formula.
But how can we test and find the shannon capacity of a new system, for example, sending an amount of data and receive it at the other end and measure the capacity.
It is obvious for BER, you just send some data and measure how many of them where failed to decode properly. But how can you find it’s capacity??
So Shannon Capacity as the name suggests is the maximum data rate that can be achieved over a particular channel. Which modulation scheme or error correction scheme you use is up to you. It is useful to know how far you are from the limit so that you know if its worth to use even more complex modulation or coding scheme. So for example if you are able to transmit 5.8 Mbps over a channel and the actual capacity is 5.9 Mbps then you can probably leave it at that. With advanced modulation schemes and strong codes such as Turbo codes modern communication systems work very close to the capacity limit.
I do not understand what you mean by “Real Capacity”.
hello guys
Can some one help me with a matlab code for antenna correlation in massive mimo.
thanx
please any one can explain how he calculate all curve ? How he get 5.36bits/sec/Hz?
Hello everyone ,
can anyone plz sugest me the way or steps to plot CDF vs Capacity graph for my Simulink MIMO-OFDM model ?
Thanks John for the response.
I also have another question. Do you know if I have real time measurements for a MIMO channel for H matrix measured with a Network Analyzer (S21 indeed) how can I normalize this data to have the correct channel capacity. Many thanks in advance
Rizwan
Hello,
I think there is an error in this code.
The SNR ‘g’ as used in the formula is in dB.
I think it must be converted to linear SNR first by 10^g/10?
Best Regards,
Rizwan
Hello,
Here g=15.8489 corresponds to an SNR of 12 dB. You can add one line for dB to linear conversion, if you want.
John
Its too good to learn….
in AWGN and Rayleigh
the for the capacity post,
i need a program for mimo ber
Sir, Sorry for raising this doubt.
I used the above said formula & got correct answer.
Sorry & Thanks again.
Sir, Thank You.
You have mentioned -channel capacity of this simple channel for an SINR of 10 dB is 5.36bits/sec/Hz. How?
sinr=10 dB
sinrlinear=10
log2(1+sinrlinear) gives 3.45
Am I doing anything wrong?
Hi Guys,
I have a problem in writing the matlab code for the following equation.
C = B.log2 [1 + SNR. |H|2] (BPS⁄ Hz)