We have previously discussed modulation and demodulation in wireless communications, now we turn our attention to channel coding. We know that in a wireless channel the transmitted information gets corrupted due to noise and fading and we get what are called bit errors. One way to overcome this problem is to transmit the same information multiple times. In coding terminology this is called a repetition code. But this is not recommended as it results in reduced data rate and reduced spectral efficiency.
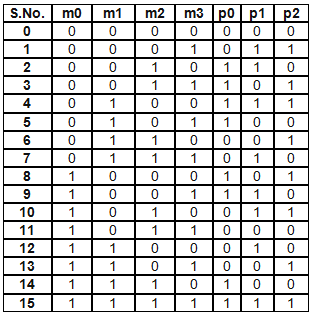
In this post we discuss Hamming (7,4) Code which transmits 4 information bits for every 7 bits transmitted, resulting in a code rate of 4/7. The 3 additional bits are called parity bits and these protect against single bit errors in the channel. This is called a systematic code since after performing the coding operation the information bits are preserved, parity bits are only appended to the information bits.
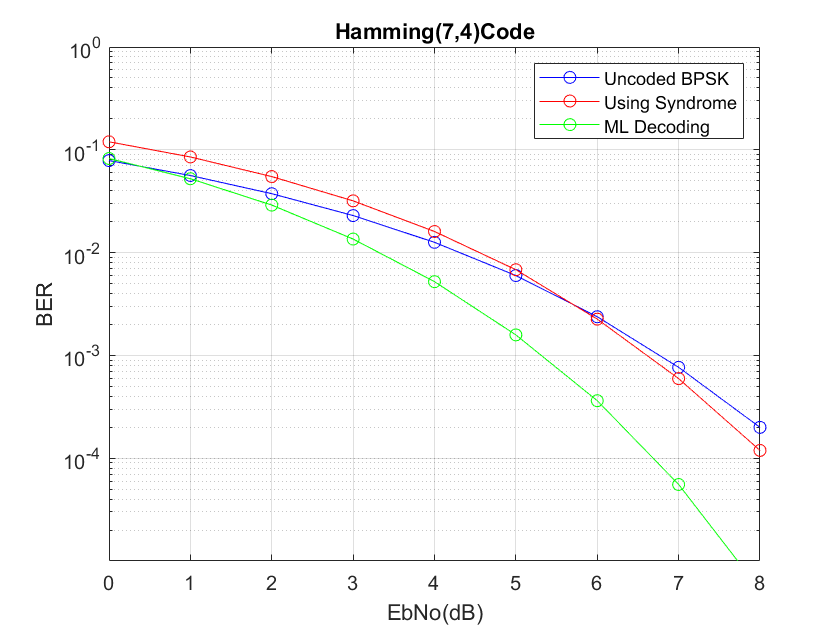
At the receiver we implement two decoding techniques namely syndrome decoding and maximum likelihood decoding and compare the bit error rate with no coding case (BPSK modulation is assumed). In the first case syndrome is calculated at the receiver, which should be all zero if no error has occurred in the transmission. If a nonzero term appears in the syndrome then it means that an error has occurred and a lookup table can be used to correct the error. It must be noted that only single bit errors can be corrected using this technique (here dmin is 3 and t=(3-1)/2).
The reason that this technique works is that the generator matrix at the transmitter is orthogonal to parity check matrix at the receiver, which is used in the calculation of syndrome. Next, we consider maximum likelihood decoding or soft decision decoding. This is a brute force method in which we search for the combination of symbols that have the minimum distance from the received symbols. This is done before the decision stage in the receiver as some information is lost in the decision stage.
The second method described above is based on Euclidean distance rather than Hamming distance. Euclidean distance is calculated between the possible transmitted symbols and the received symbols whereas Hamming distance is calculated between the possible transmitted bits and received bits. As expected, maximum likelihood decoding performs much better than syndrome-based decoding which can detect only one bit error at a time. In fact, at low signal to noise ratio syndrome-based method is even worse than no coding case.
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% ENCODING AND DECODING USING HAMMING CODE
% k is the number of message bits
% n is the number of encoded bits
% k/n is the code rate
% Copyright 2020 RAYmaps
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clear all
close all
k=4;
n=7;
m=round(rand(1,k));
P=[1 0 1;
1 1 1;
1 1 0;
0 1 1];
I=eye(k);
G=[I,P];
c=mod(m*G,2);
cx=2*c-1;
Eb=1.0*(n/k);
EbNo=10;
sigma=sqrt(Eb/(2*EbNo));
y=cx+sigma*randn(1,n);
d=y>0;
H=[P',eye(n-k)];
s=mod(d*H',2);
if s==([1 0 1])
d(1)=not(d(1));
elseif s==([1 1 1])
d(2)=not(d(2));
elseif s==([1 1 0])
d(3)=not(d(3));
elseif s==([0 1 1])
d(4)=not(d(4));
end
ber=sum(d(1:4)~=m)/4;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Note:
- We have assumed BPSK modulation in the simulations but any other modulation format can be easily incorporated. In reality channel coding provides the leverage to go higher modulation formats, resulting in higher spectral efficiency.
- Single bit errors only need to be corrected for the four possible erroneous message sequences. Errors in parity bits can be ignored since they do not influence the bit error rate.
- Hard decision decoding does not make full use of the information available e.g. if we have BPSK modulation (s=+/-1) there is no difference between a +0.1 and +0.5 after a bit decision is made. But soft decision decoding gives more weightage to +0.5 than +0.1.