Omar Khayyam was a Muslim mathematician and poet of the 11th and 12th centuries (1048-1131). His poetic works known as Rubaiyat of Omar Khayyam were translated from Persian to English and made popular by Edward Fitzgerald in the late nineteenth century. In the field of mathematics his most valuable contribution was the solution he presented to the cubic equations using geometrical methods. Some of this was adapted from earlier works by Greeks but his compilation of the various cases and their solutions was most complete.
Lets assume that the cubic equation also known as the third degree equation (highest power of the unknown variable) is of the form:
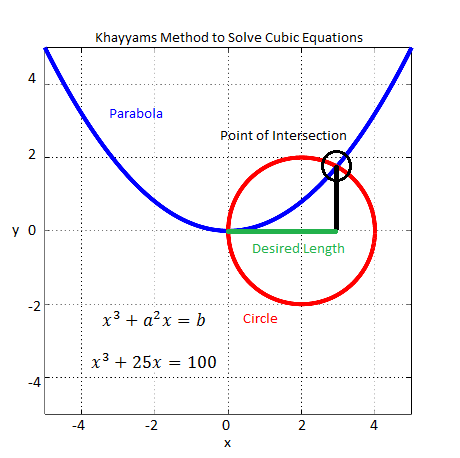
x3+a2x=b
Khayyam’s method consisted of constructing a parabola with equation x2=ay and a circle with center (b/2a2,0) and radius b/2a2. Then the x-coordinate of the intersection of the circle and the parabola gives the solution to the cubic equation. The root found by this method is the real and positive root since the length of a line segment cannot be negative or imaginary. These cases (negative and imaginary roots) were not discussed by Khayyam and were worked out much later by other mathematicians. The MATLAB code for this geometrical construction is given below.
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Omar Khayyams Method to Find
% the Roots of a Cubic Equation
%
% Copyright RAYmaps 2017 (YA)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clear all
close all
% Plot the parabola
a =5;
x =-5:0.01:5;
y =(x.^2)/a;
plot(x,y,'linewidth',4);
hold on
% Plot the circle
b =100;
d =b/(a.^2);
r =d/2;
t =0:pi/180:2*pi;
plot(r+r*cos(t), r*sin(t),'r', 'linewidth', 4);
hold off
axis([-5 5 -5 5], "square")
grid on
title('Khayyams Method to Solve Cubic Equations')
xlabel('x')
ylabel('y')
Omar Khayyam’s Method for Solving Cubic Equations
Notes:
- For more on origins of geometrical methods see the following post on Al-Khwarizmi.
- For an interactive tool to understand the method of Omar Khayyam visit the following page.
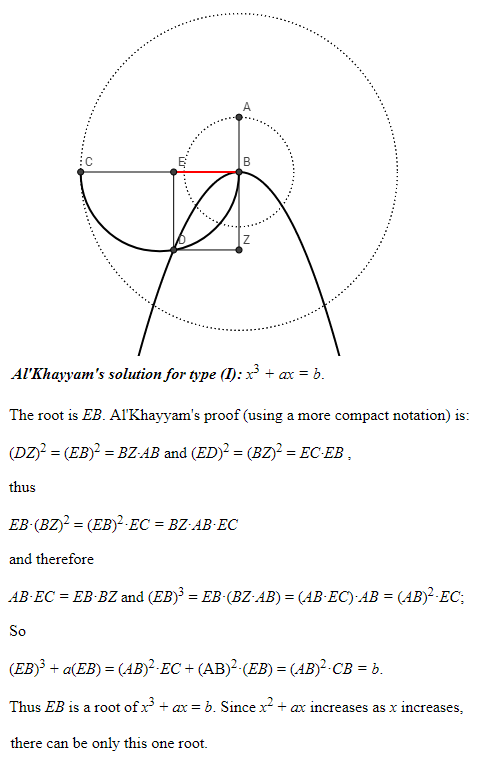
- For a proof of validity of Khayyam’s method see the following page on Cornell website or see selected abstract below. Please note slightly different form of the equation where the term a2 has been replaced by a. This is just a constant term and either form works.
Author: Yasir
More than 20 years of experience in various organizations in Pakistan, the USA, and Europe. Worked with the Mobile and Portable Radio Group (MPRG) of Virginia Tech and Qualcomm USA and was one of the first researchers to propose Space Time Block Codes for eight transmit antennas. Have publsihed a book “Recipes for Communication and Signal Processing” through Springer Nature.
2 thoughts on “Omar Khayyam’s Solution to Cubic Equations”
Excellent One , It would be interesting to Know how Muslim scientists who were at the top the world from 8th century to 12th Century lost their relevance. Was It that they were Polymaths and not specialist and lived in the era when Polymaths had more value than specialist
I think there were a few reasons. Destruction of Baghdad by Mongols was one reason. In fighting among the spreading Muslim empire was another. Also, Europeans were quick to learn and built on the new theories emanating from the Muslim world.