Al Khwarizmi was a Muslim scholar who worked under the patronage of emperor Al Mamun in the 9th century in Baghdad. Al Mamun like his father was interested in supporting learning and formed the House of Wisdom of which Al Khwarizmi was a part. It was here that Greek philosophical and scientific works were translated into Arabic. In recognition of his support Al Khwarizmi dedicated two of his works on algebra and astronomy to the great emperor. His treatise known as Hisab al-jabr w’al-muqabala was the most famous and important one and was translated into several other languages. Over the years al-jabr came to be known as algebra and Al Khwarizmi (Algoritmi in Latin) became algorithm.
According to Al Khwarizmi equations are linear or quadratic and are composed of units, roots and squares. To Al Khwarizmi a unit was a number, a root was x and a square was x2. He defined two basic operations to solve equations namely al-jabr (the process of removing negative terms from an equation) and al-muqabala (the process of reducing positive terms of the same power when they occur on both sides of an equation). All Al Khwarizmi mathematics was done entirely in words and no symbol was used e.g. he solves an equation x2+10x=39 as follows:
“… a square and 10 roots are equal to 39 units. The question therefore in this type of equation is about as follows: what is the square which combined with ten of its roots will give a sum total of 39? The manner of solving this type of equation is to take one-half of the roots just mentioned. Now the roots in the problem before us are 10. Therefore take 5, which multiplied by itself gives 25, an amount which you add to 39 giving 64. Having taken then the square root of this which is 8, subtract from it half the roots, 5 leaving 3. The number three therefore represents one root of this square, which itself, of course is 9. Nine therefore gives the square”
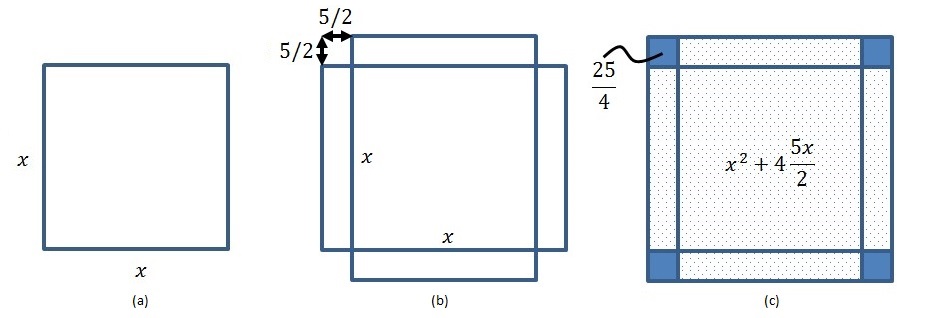
One of his masterpieces is his method of solving equations using simple geometry, as shown above. For example to solve the equation x2+10x = 39 he first creates a square with length of each side equal to x and area x2. He then adds 10x to it by creating four rectangles of area 10x/4 = 5x/2 each. Thus the lightly shaded area in figure (c) above represents x2+10x or 39. Now we add the areas of the four corners (darkly shaded) to get x2+10x+25 or 64 (39+25). So we find out that the side of the larger square is of length 8 (square root of 64). But we already know that the length of a side is 5/2+x+5/2 = x+5. So we have the final equation x+5 = 8 or x = 3.
Author: Yasir
More than 20 years of experience in various organizations in Pakistan, the USA, and Europe. Worked with the Mobile and Portable Radio Group (MPRG) of Virginia Tech and Qualcomm USA and was one of the first researchers to propose Space Time Block Codes for eight transmit antennas. Have publsihed a book “Recipes for Communication and Signal Processing” through Springer Nature.
One thought on “Al Khwarizmi’s Method of Solving Equations in One Variable”