Equal Gain Combining in Rayleigh Fading

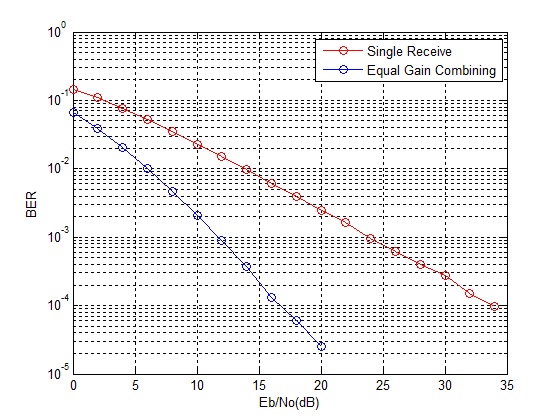
When wireless signals travel from a single transmit antenna to multiple receive antennas they experience different fading conditions. While signal from one path may experience a deep fade the signal from another path may be stronger. Therefore selecting the stronger of the two signals (selection combining, threshold combining) or adding the signals (equal gain combining, maximal ratio combining) would always yield much better results (lower bit error rate). However, there must be sufficient spacing between the different receive antennas for the received signals to be dissimilar (uncorrelated). In the simulation below we consider a 1-Tx, 2-Rx scenario. The signals arriving at the two receive antennas are added together before detection.

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function[ber]=err_rate4(l,EbNo)
si=2*(round(rand(1,l))-0.5);
sq=2*(round(rand(1,l))-0.5);
s=si+j*sq;
n1=(1/sqrt(2*10^(EbNo/10)))*(randn(1,l)+j*randn(1,l));
h1=(1/sqrt(2))*((randn(1,l))+j*(randn(1,l)));
n2=(1/sqrt(2*10^(EbNo/10)))*(randn(1,l)+j*randn(1,l));
h2=(1/sqrt(2))*((randn(1,l))+j*(randn(1,l)));
r1=abs(h1).*s+n1;
r2=abs(h2).*s+n2;
r=r1+r2;
si_=sign(real(r));
sq_=sign(imag(r));
ber1=(l-sum(si==si_))/l;
ber2=(l-sum(sq==sq_))/l;
ber=mean([ber1 ber2]);
return
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

Note:

1. Not only the signals on the two paths experience uncorrelated fading but the the noise at the receiver front ends is also uncorrelated.

2. In reality the signals over both the paths would also experience random phase shifts but these can be removed before the combining process at the receiver.

Author: Yasir

More than 20 years of experience in various organizations in Pakistan, the USA, and Europe. Worked with the Mobile and Portable Radio Group (MPRG) of Virginia Tech and Qualcomm USA and was one of the first researchers to propose Space Time Block Codes for eight transmit antennas. Have publsihed a book “Recipes for Communication and Signal Processing” through Springer Nature.

Twitter Facebook Linkedin