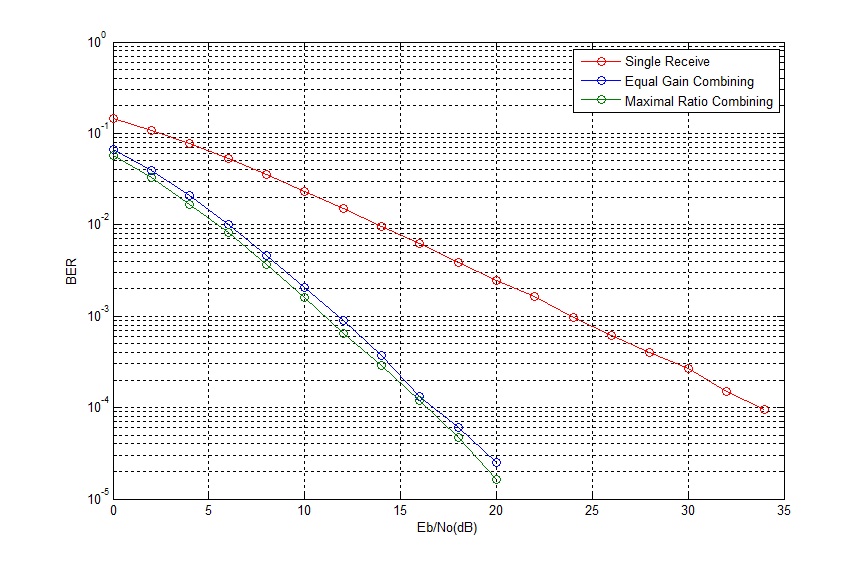
We just saw the advantage an equal gain combiner (a combining scheme that just adds the signals after co-phasing them) provides in a Rayleigh fading channel. Lets now look at a variant of this scheme called maximal ratio combining (MRC). In MRC the signals arriving at the receivers are weighted by the channel gains i.e. a stronger signal is weighted more than a weaker signal before combining. It must be noted that in an actual system the received signals are both scaled and phase shifted thus an MRC receiver multiplies the received signals by the complex conjugate of the channel coefficients before addition.
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function[ber]=err_rate4(l,EbNo)
si=2*(round(rand(1,l))-0.5);
sq=2*(round(rand(1,l))-0.5);
s=si+j*sq;
n1=(1/sqrt(2*10^(EbNo/10)))*(randn(1,l)+j*randn(1,l));
h1=(1/sqrt(2))*((randn(1,l))+j*(randn(1,l)));
n2=(1/sqrt(2*10^(EbNo/10)))*(randn(1,l)+j*randn(1,l));
h2=(1/sqrt(2))*((randn(1,l))+j*(randn(1,l)));
r1=abs(h1).*s+n1;
r2=abs(h2).*s+n2;
r=abs(h1).*r1+abs(h2).*r2;
si_=sign(real(r));
sq_=sign(imag(r));
ber1=(l-sum(si==si_))/l;
ber2=(l-sum(sq==sq_))/l;
ber=mean([ber1 ber2]);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
OR (using the complex channel coefficient)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function[ber]=err_rate4(l,EbNo)
si=2*(round(rand(1,l))-0.5);
sq=2*(round(rand(1,l))-0.5);
s=si+j*sq;
n1=(1/sqrt(2*10^(EbNo/10)))*(randn(1,l)+j*randn(1,l));
h1=(1/sqrt(2))*((randn(1,l))+j*(randn(1,l)));
n2=(1/sqrt(2*10^(EbNo/10)))*(randn(1,l)+j*randn(1,l));
h2=(1/sqrt(2))*((randn(1,l))+j*(randn(1,l)));
r1=h1.*s+n1;
r2=h2.*s+n2;
r=conj(h1).*r1+conj(h2).*r2;
si_=sign(real(r));
sq_=sign(imag(r));
ber1=(l-sum(si==si_))/l;
ber2=(l-sum(sq==sq_))/l;
ber=mean([ber1 ber2]);
return
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
We see that there is an incremental improvement in BER using MRC instead of EGC (1dB can sometimes be significant).
Note:
1. The performance of MRC is the same using both the techniques given above.
2. Phase rotation of the noise component does not effect the BER performance.
Author: Yasir
More than 20 years of experience in various organizations in Pakistan, the USA, and Europe. Worked with the Mobile and Portable Radio Group (MPRG) of Virginia Tech and Qualcomm USA and was one of the first researchers to propose Space Time Block Codes for eight transmit antennas. Have publsihed a book “Recipes for Communication and Signal Processing” through Springer Nature.