Category Archives: Modulation

MSK, QAM, OFDM

OFDM Modulation and Demodulation (AWGN) – II

5G, BER Performance, LTE, Modulation, WiMAX

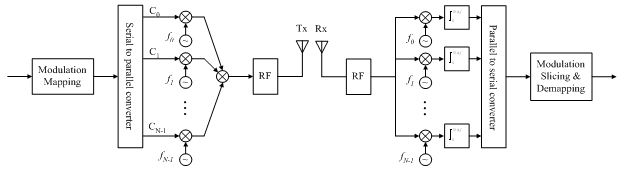
We have previously looked at a simple OFDM modulation and demodulation scheme. We saw that the BER performance of OFDM in AWGN was the same as the BER performance of the underlying modulation scheme (QPSK in this case). We will now continuously improve upon our basic simulation to get a more realistic picture. In this regard we introduce the cyclic prefix which is used in OFDM to overcome Intersymbol Interference. The duration of the cyclic prefix is 0.8usec (16 samples at 20MHz) resulting in a symbol duration of 4usec (IEEE 802.11a). Given below is the code for OFDM modulation and demodulation with cyclic prefix.

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% FUNCTION TO CALCULATE BER OF OFDM IN AWGN
% seq_len: Input, number of OFDM symbols
% n_carr: Input, number of subcarriers 
% EbNo: Input, energy per bit to noise PSD
% ber: Output, bit error rate
% Copyright RAYmaps (www.raymaps.com)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function[ber]=OFDM_err(seq_len,n_carr,EbNo)
n_pre=16;                                                             
n_tot=n_carr+n_pre;                                                   
for n=1:seq_len
si=2*(round(rand(1,n_carr))-0.5);                                     
sq=2*(round(rand(1,n_carr))-0.5);                                              
s=si+j*sq;                                                            
s_ofdm=sqrt(n_carr)*ifft(s,n_carr);                                   
s_cyc=sqrt(n_carr/n_tot)*([s_ofdm(49:64),s_ofdm]);                    
wn=(1/sqrt(2*10^(EbNo/10)))*(randn(1,n_tot)+j*randn(1,n_tot));        
r=s_cyc+wn;                                                           
r_ext=r(17:80);                                                       
s_est=fft(r_ext,n_carr);                                              
si_est=sign(real(s_est));                                             
sq_est=sign(imag(s_est));                                             
ber1(n)=(n_carr-sum(si==si_est))/n_carr;                              
ber2(n)=(n_carr-sum(sq==sq_est))/n_carr;                               
end
ber=mean([ber1 ber2]);                                                
return
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

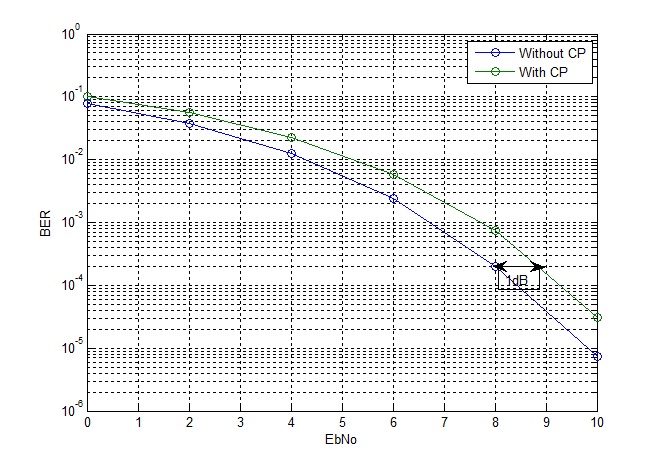
Since the number of samples is increased from 64 to 80 their is an increase in symbol energy. Therefore the signal level needs to be scaled by a factor of sqrt(64/80) to keep the total symbol energy to be the same. This results in approximately 1dB of loss in BER performance as shown in the figure below.

OFDM BER

OFDM Modulation and Demodulation (AWGN)

5G, BER Performance, LTE, Modulation, WiMAX, ,

OFDM modulation works on the principle of converting a serial symbol stream to a parallel symbol stream with each symbol from the parallel set modulating a seperate carrier. The spacing between the carriers is 1/T where T is the duration of the OFDM symbols (without cyclic prefix). This guarantees orthogonality of the carriers i.e. there is no interference between carriers. The addition of orthogonal carriers modulated by parallel symbol streams is equivalent to taking the IFFT of the parallel symbol set. At the receiver the inverse operation of FFT is performed and the parallel symbol streams are converted to serial symbol streams.

The main advantage of this scheme is that one carrier (or set of carriers) may undergo severe fading but other carriers would be able to carry data. Equalization on these narrowband channels is also much easier than equalization of one wideband channel. Intersymbol Interference (ISI) which effects the signal in the time domain is removed by adding a guard period between symbols, called cyclic prefix (which we will discuss later).

OFDM Modulator Demodulator

We demonstrate the performance of OFDM with QPSK modulation in a simple AWGN channel. Although the true benefits of OFDM are really visible when we have a fading channel but this simple example would serve as a good starting point.

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% FUNCTION TO CALCULATE BER OF OFDM IN AWGN
% seq_len: Input, number of OFDM symbols
% n_carr: Input, number of subcarriers 
% EbNo: Input, energy per bit to noise PSD
% ber: Output, bit error rate
% Copyright RAYmaps (www.raymaps.com)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function[ber]=OFDM_err(seq_len,n_carr,EbNo)
for n=1:seq_len
si=2*(round(rand(1,n_carr))-0.5);
sq=2*(round(rand(1,n_carr))-0.5);
s=si+j*sq;
s_ofdm=sqrt(n_carr)*ifft(s,n_carr);
wn=(1/sqrt(2*10^(EbNo/10)))*(randn(1,n_carr)+j*randn(1,n_carr));
r=s_ofdm+wn;
s_est=fft(r,n_carr);
si_est=sign(real(s_est));
sq_est=sign(imag(s_est));
ber1(n)=(n_carr-sum(si==si_est))/n_carr;
ber2(n)=(n_carr-sum(sq==sq_est))/n_carr;
end
ber=mean([ber1 ber2]);                                                           
return
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
OFDM BER AWGN

As expected in an AWGN channel the BER performance of OFDM is simply the BER performance of QPSK in AWGN. With cyclic prefix, some of the transmitted energy would be wasted and the BER performance would be a bit worse (to be discussed in future posts).