The real benefits of OFDM become apparent in a frequency selective channel. The introduction of the cyclic prefix (guard period) allows us to remove the Intersymbol Interference (ISI) in the time domain and frequency domain equalization allows us to overcome the channel variations in the frequency domain.

We consider a simple FIR filter for our channel model with coefficients ht=[0.8 0.54 0.24 0.10 0.04]. This is a simplistic approach since the channel coefficients are all real which means that all multipath components are co-phase. To model a more realistic channel we then introduce a uniform phase shift to all the channel coefficients.

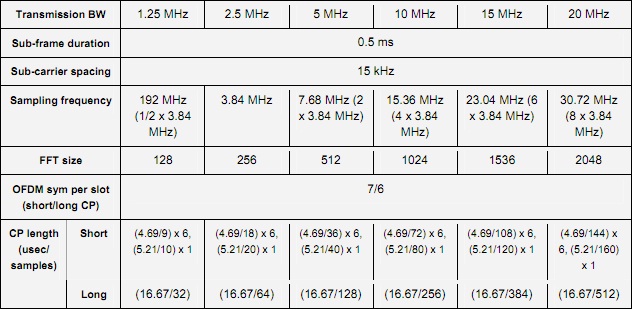
We use an FFT size of 128 and cyclic prefix of 32 samples (16.67usec) in the simulation given below.

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% FUNCTION TO SIMULATE THE PERFORMANCE OF 64-QAM OFDM IN STATIC FREQUENCY SELECTIVE CHANNEL
% n_bits: Input, length of binary sequence
% n_fft: Input, length of FFT (Fast Fourier Transform)
% EbNodB: Input, energy per bit to noise power spectral density ratio
% ber: Output, bit error rate
% Copyright RAYmaps (www.raymaps.com)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function[ber]= M_QAM_OFDM_fading(n_bits,n_fft,EbNodB)

Eb=7;
M=64;
k=log2(M);
n_cyc=32;
EbNo=10^(EbNodB/10);
x=transpose(round(rand(1,n_bits)));
h1=modem.qammod(M);
h1.inputtype='bit';
h1.symbolorder='gray';
y=modulate(h1,x);
n_sym=length(y)/n_fft;

for n=1:n_sym;
    s_ofdm=sqrt(n_fft)*ifft(y((n-1)*n_fft+1:n*n_fft),n_fft);
    s_ofdm_cyc=[s_ofdm(n_fft-n_cyc+1:n_fft); s_ofdm];
    ht=[0.8 0.54 0.24 0.10 0.04];
    Hf=fft(ht,n_fft);
    r_ofdm_cyc=conv(s_ofdm_cyc,ht);
    r_ofdm_cyc=(r_ofdm_cyc(1:n_fft+n_cyc));
    wn=sqrt((n_fft+n_cyc)/n_fft)*(randn(1,n_fft+n_cyc)+j*randn(1,n_fft+n_cyc));
    r_ofdm_cyc=r_ofdm_cyc+sqrt(Eb/(2*EbNo))*wn.';
    r_ofdm=r_ofdm_cyc(n_cyc+1:n_fft+n_cyc);
    s_est((n-1)*n_fft+1:n*n_fft)=(fft(r_ofdm,n_fft)/sqrt(n_fft))./Hf.';
end

h2=modem.qamdemod(M);
h2.outputtype='bit';
h2.symbolorder='gray';
h2.decisiontype='hard decision';
z=demodulate(h2,s_est.');
ber=(n_bits-sum(x==z))/n_bits
return
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

We also have accounted for the extra energy transmitted for the cyclic prefix in our signal to noise calibration.

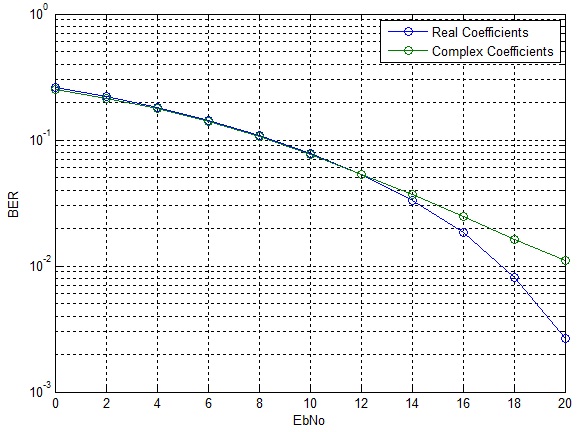
It can be seen that up to 12dB the BER performance for the two cases is quite similar, however, after 12dB the BER for the real case drops significantly whereas the BER for the complex case goes down in linear fashion. The error rate can be significantly improved by employing channel coding and antenna diversity schemes.

Author: Yasir Ahmed (aka John)

More than 20 years of experience in various organizations in Pakistan, the USA, and Europe. Worked as a Research Assistant within the Mobile and Portable Radio Group (MPRG) of Virginia Tech and was one of the first researchers to propose Space Time Block Codes for eight transmit antennas. The collaboration with MPRG continued even after graduating with an MSEE degree and has resulted in 12 research publications and a book on Wireless Communications. Worked for Qualcomm USA as an Engineer with the key role of performance and conformance testing of UMTS modems. Qualcomm is the inventor of CDMA technology and owns patents critical to the 4G and 5G standards.

Twitter Facebook Linkedin