Most of intermediate Physics courses present Snell’s law of refraction in one form or another. But a little known mathematician with the name Ibn Sahl (c. 940–1000) found this law about 650 years before Snell (Willebrord Snellius c. 1580–1626). This mathematical expression was lost for centuries until some scholars recently were able to dig it up from historical records. Even Ibn al-Haytham (author of Book of Optics or Kitab ul Manazir) who came to the fore a few years later did not recognize the brilliance of Ibn Sahl’s simple expression.
Ibn Sahl was aware that Greek’s knew that there was a relationship between the angle of incidence and angle of refraction of a ray traveling from one medium to the other. They thought that ratio of the two angles was a constant i.e. if the angle of incidence was doubled the angle of refraction also doubled. This also meant that the arcs formed by the two angles on a circle centered at the point of incidence were also directly related (in a linear relationship). But Ibn Sahl showed that this was incorrect.
Ibn Sahl showed that it was not the angles but the sine of the angles that were linearly related. We explain it with the help of the figure below. Imagine that a ray of light travels from air to a denser medium (such as water), then the ray bends towards the normal and angle of refraction is smaller than angle of incidence. According to Ibn Sahl the ratio of line segments l1 and l2 as shown in the figure is a constant. This in fact means that the two sines have a constant ratio and this is equal to refractive index of the second medium (n2) with refractive index of air almost equal to 1 (n1).
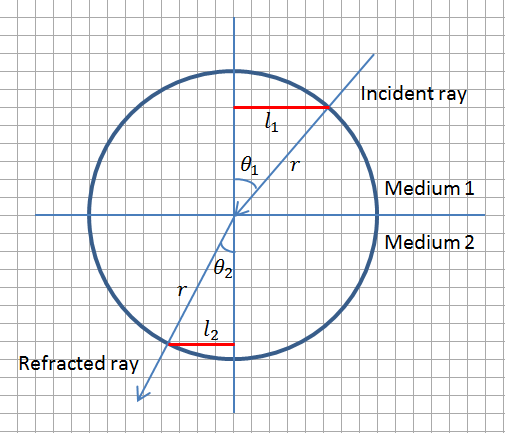
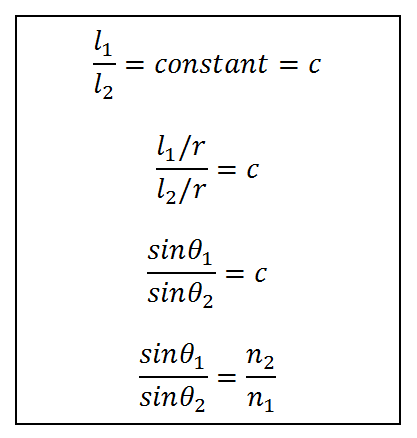
Ibn Sahl was not aware of the parameter ‘n’ defined as refractive index by later scientists. Also, as is known that for small angles, sine of the angle and angle itself are almost the same, so earlier scientists like Ptolemy might have been tricked into assuming that the angles are directly related. This can be understood by looking at the figure above. If the angle of incidence is continuously reduced, the angle of refraction would also decrease and the lengths of the two line segments in red (l1 and l2) would approach the lengths of the arcs that are formed between the ray and the normal.
Note: Roshdi Rashed found the Ibn Sahl text to have been dispersed in manuscripts in two different libraries, one in Tehran, and the other in Damascus. He reassembled the surviving portions, translated and published them as “Geometry and dioptric in the tenth century: Ibn Sahl, al-Quhi and Ibn al-Haytham”.
Author: Yasir
More than 20 years of experience in various organizations in Pakistan, the USA, and Europe. Worked with the Mobile and Portable Radio Group (MPRG) of Virginia Tech and Qualcomm USA and was one of the first researchers to propose Space Time Block Codes for eight transmit antennas. Have publsihed a book “Recipes for Communication and Signal Processing” through Springer Nature.