Quadrature Amplitude Modulation has been adopted by most wireless communication standards such as WiMAX and LTE. It provides higher bit rates and consequently higher spectral efficiencies. It is usually used in conjunction with Orthogonal Frequency Division Multiplexing (OFDM) which provides a simple technique to overcome the time varying frequency selective channel.
We have previously discussed the formula for calculating the bit error rate (BER) of QAM in AWGN. We now calculate the same using a simple Monte Carlo Simulation.
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% FUNCTION THAT CALCULATES THE BER OF M-QAM IN AWGN
% n_bits: Input, number of bits
% M: Input, constellation size
% EbNodB: Input, energy per bit to noise power spectral density
% ber: Output, bit error rate
% Copyright RAYmaps (www.raymaps.com)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function[ber]= QAM_AWGN(n_bits, M, EbNodB)
% Transmitter
k=log2(M);
EbNo=10^(EbNodB/10);
x=transpose(round(rand(1,n_bits)));
h1=modem.qammod(M);
h1.inputtype='bit';
h1.symbolorder='gray';
y=modulate(h1,x);
% Channel
Eb=mean((abs(y)).^2)/k;
sigma=sqrt(Eb/(2*EbNo));
w=sigma*(randn(1,n_bits/k)+1i*randn(1,n_bits/k));
r=y+w';
% Receiver
h2=modem.qamdemod(M);
h2.outputtype='bit';
h2.symbolorder='gray';
h2.decisiontype='hard decision';
z=demodulate(h2,r);
ber=(n_bits-sum(x==z))/n_bits
return
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
The above function basically has three inputs and one output. The inputs are the number of bits to be passed through the channel, the size of the constellation and the signal to noise ratio in dB. The output is the bit error rate (BER). The simulation can be divided into three section namely the transmitter, the channel and the receiver. In this simulation we have used Gray coding which gives us about a dB of improvement at low to medium signal to noise ratio.
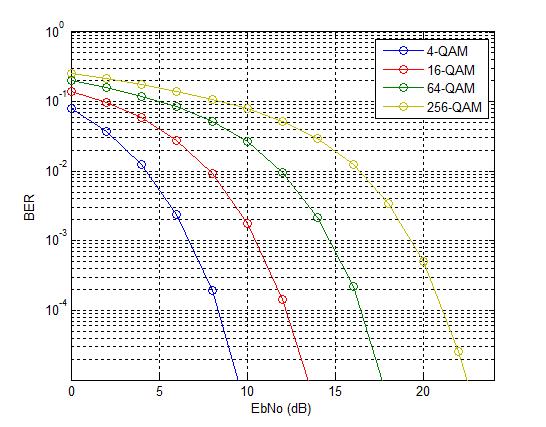
As seen above the BER obtained through our simulation matches quite well with the BER obtained through the theoretical formula. Each additional bit per symbol required about 2dB extra in signal to noise ratio to achieve the same bit error rate.
Lastly we explain some of the terms used above.
AWGN
All wireless receivers suffer from thermal noise which is a function of absolute temperature and bandwidth of the receiver. This noise is added to the received signal and makes detection of weak signals a major challenge. Just to given you an idea typical GSM receivers have a noise floor of -113 dBm. Therefore, if the received signal has a power of -100 dBm we get a signal to noise ratio (SNR) of 13 dB. In simulation this noise is usually modeled as a Gaussian Random Process. It is additive, as opposed to channel impairments which are multiplicative and has a flat spectrum (thus called White Noise).
Gray Coding
When using QAM modulation, each QAM symbol represents 2,3,4 or higher number of bits. That means that when a symbol error occurs a number of bits are reversed. Now a good way to do the bit-to-symbol assignment is to do it in a way such that no neighboring symbols differ by more than one bit e.g. in 16-QAM, a symbol that represents a binary word 1101 is surrounded by four symbols representing 0101, 1100, 1001 and 1111. So if a symbol error is made, only one bit would be in error. However, one must note that this is true only in good signal conditions. When the SNR is low (noise has a higher magnitude) the symbol might be displaced to a location that is not adjacent and we might get higher number of bits in error.
Hard Decision
The concept of hard decision decoding is important when talking about channel coding, which we have not used in the above simulation. However, we will briefly explain it here. Hard decision is based on what is called “Hamming Distance” whereas soft decision is based on what it called “Euclidean Distance”. Hamming Distance is the distance of a code word in binary form, such as 011 differs from 010 and 001 by 1. Whereas the Euclidean distance is the distance before a decision is made that a bit is zero or one. So if the received sequence is 0.1 0.6 0.7 we get a Euclidean distance of 0.8124 from 010 and 0.6782 from 001. So we cannot make a hard decision about which sequence was transmitted based on the received sequence of 011. But based on the soft metrics we can make a decision that 001 was the most likely sequence that was transmitted (assuming that 010 and 001 were the only possible transmitted sequences).
Author: Yasir
More than 20 years of experience in various organizations in Pakistan, the USA, and Europe. Worked with the Mobile and Portable Radio Group (MPRG) of Virginia Tech and Qualcomm USA and was one of the first researchers to propose Space Time Block Codes for eight transmit antennas. Have publsihed a book “Recipes for Communication and Signal Processing” through Springer Nature.
16 thoughts on “M-QAM Bit Error Rate in AWGN”
Hi John.
Thanks for your guide.
I tried to use the code you posted above but got this error
“Unable to resolve the name modem.qammod.”
Can you tell me the version of Matlab you are using?
Hi,
Do you have the communication toolbox installed. Also, check the posts on OFDM, where I updated some code as I was also getting error messages.
Cheers
Hi John, I cant seem to run the code you posted above. An error appeared saying “Unable to resolve the name modem.qammod.” Do you know what the problem is?
Are you using MATLAB or Octave? Octave does not have all the functions…
hi john i want to make QAM_AWGN for calculating BER how i can make in simple waye can you help me sir
Hi Abdullah,
Just use the code I have given above. If you do not know how to use a function look up MATLAB help…if you still do not understand let me know…
Hi John, is it possible to increase the bit rate by increasing the bandwidth, without exceeding the theoretical limit for the bpsk? for example with a bit rate of 5 bits/s over a bandwidth of 5 Hz . This is correct? And if so how can I implement it in matlab code? Do you have any idea?
Thanks again for attention !
Hi Fred, I do not think I fully understand your question. A simple answer is that you can increase the bit rate by increasing the bandwidth but remember that increasing the bandwidth also increases the noise power as noise power is equal to Noise Power Spectral Density (PSD) times the bandwidth.
John
Hi John,
I’m working to a bpsk ber simulation and I have to increase the spectral efficiency, putting the symbol rate (or baud rate) in the code! Can you help me in some way? Need help, I can’t understand how to increase the number of bit for symbol in the code!
Code:
Num_bit = 10^6 % number of bits
data = rand(1,Num_bit)>0.5; % random bits generator
s = 2*data-1; % bpsk modulation
noise = 1/sqrt(2)*[randn(1,Num_bit) + j*randn(1,Num_bit)]; % add gaussian noise (Channel AWGN)
Ebno = [0:10]; % Unitary variance
for i = 1:length(Ebno)
% adding noise
rx = s + 10^(-Ebno(i)/20)*noise;
% receiver
datarx = real(rx)>0; % hard decision, if real(rx) > 0 datarx = 1, else datarx = 0
num_err(i) = size(find([data- datarx]),2);
end
media = mean(data);
varianza = var (noise);
fprintf (‘media = %f\n’, media);
fprintf (‘varianza = %f\n’, varianza);
% simulation BER
BER = num_err/Num_bit;
teoBer = 0.5*erfc(sqrt(10.^(Ebno/10)));
figure
semilogy(Ebno,teoBer,’b.-‘);
hold on
semilogy(Ebno,BER,’r-‘);
axis([0 10 10^-5 0.5])
grid on
legend(‘teorico’, ‘simulato’);
xlabel(‘Eb/No, dB’);
ylabel(‘Bit Error Rate’);
title(‘Curva di BER per modulazione BPSK’);
Fred,
Your code seems to be working fine. I am not sure what your question is. Now that you have done BPSK modulation and demodulation you can move to QPSK (2 bits per symbol instead of 1). You can get some help here.
http://www.raymaps.com/index.php/bit-error-rate-of-qpsk/
John
Hi John,
I don’t speak English well. 🙂
Please! You can explain difference between function AWGN (in matlab) and code
“Eb=mean((abs(y)).^2)/k;
sigma=sqrt(Eb/(2*EbNo));
w=sigma*(randn(1,n_bits/k)+1i*randn(1,n_bits/k));”
As I understand it, function AWGN in matlab adds gaussian noise and when I try it in code I get incorrect results.
mail: manhdatbn93@gmail.com
Thank you 🙂
The above code calculates the energy per bit and then calculates the noise power to get the desired signal to noise ratio. For working of AWGN use MATLAB help.
John
Pooja,
I hope you have created two files.
1. The above code with the name QAM_AWGN.m
2. A piece of code that is used to call the above function as
BER=QAM_AWGN(n_bits, M, EbNodB)
Hope this helps!!!
John
Pooja,
You have to take care of the input arguments in
QAM_AWGN(n_bits, M, EbNodB)
such as
QAM_AWGN(100000, 16, 10)
this means that the Bit Error Rate (BER) is calculated for 100000 bits, for 16-QAM at an EbNo of 10dB.
Try it!!!
John
Hi
I tried your code for QAM_AWGN but on the second line it is showing me error:Not enough input arguments. Can you help me?
To Mr John
Greeting,
Nice to know you. I’m planning to do a research about performance of wimax/lte downlinks over haps channel in terms of capacity vs HAP elevation angle. Could you please provide some matlab scripts related to this topic. I look forward to your help.
thanks!