Fast Fourier Transform – Code

Most of us have used the FFT routine in MATLAB. This routine has become increasingly important in simulation of communication systems as it is being used in Orthogonal Frequency Division Multiplexing (OFDM) which is employed in 4G technologies like LTE and WiMAX. We would not go into the theoretical details of the FFT, rather, we would produce the MATLAB code for it and leave the theoretical discussion for a later time.

The underlying technique of the FFT algorithm is to divide a big problem into several smaller problems which are much easier to solve and then combine the results in the end.

%%%%% INITIALIZATION %%%%%
clear all
close all

fm=100;
fs=1000;
Ts=1/fs;
nn=1024;
isign=1;

t=0:Ts:(nn-1)*Ts;

x_c=exp(1i*2*pi*fm*t);
x(1:2:2*nn-1)=imag(x_c);
x(2:2:2*nn)=real(x_c);

%%%%% BIT REVERSAL %%%%%
n=2*nn;
j=1;
for i=1:2:n-1
    if(j>i)
        temp=x(j);
        x(j)=x(i);
        x(i)=temp;

        temp=x(j+1);
        x(j+1)=x(i+1);
        x(i+1)=temp;
    end
    m=nn;
    while (m >= 2 && j > m)
        j=j-m;
        m=m/2;
    end
    j=j+m;
end

%%%%% DANIELSON-LANCZOS ALGO %%%%%
mmax=2;
while (n > mmax)
    istep=2*mmax;
    theta=isign*(2*pi/mmax);
    wtemp=sin(0.5*theta);
    wpr=-2*wtemp*wtemp;
    wpi=sin(theta);
    wr=1.0;
    wi=0.0;
    for m=1:2:mmax-1
        for i=m:istep:n
            j=i+mmax;
            tempr=wr*x(j)-wi*x(j+1);
            tempi=wr*x(j+1)+wi*x(j);
            x(j)=x(i)-tempr;
            x(j+1)=x(i+1)-tempi;
            x(i)=x(i)+tempr;
            x(i+1)=x(i+1)+tempi;
        end
        wtemp=wr;
        wr=wr*wpr-wi*wpi+wr;
        wi=wi*wpr+wtemp*wpi+wi;
    end
mmax=istep;
end
F=x(2:2:n)+1i*x(1:2:n-1);
plot((0:fs/(nn-1):fs),abs(F))

In the above example we have calculated an ‘nn’ point complex FFT of an ‘nn’ point complex time domain signal. The algorithm takes the input in a special arrangement where the ‘nn’ point complex input signal is converted into ‘2*nn’ real sequence where the imaginary components are placed in odd elements and real components are placed in even elements of the input sequence. A similar arrangement works for the output sequence.

Shown below is the FFT of a complex exponential with a frequency of 100 Hz. The plot is shown from 0Hz to 1000 Hz which is the sampling frequency. A signal with multiple frequencies would have to be passed through a Low Pass Filter (LPF) so that the signal components above 500 Hz (fs/2) are filtered out. When the FFT of a real signal is performed an image frequency is produced between 500 Hz to 1000 Hz.

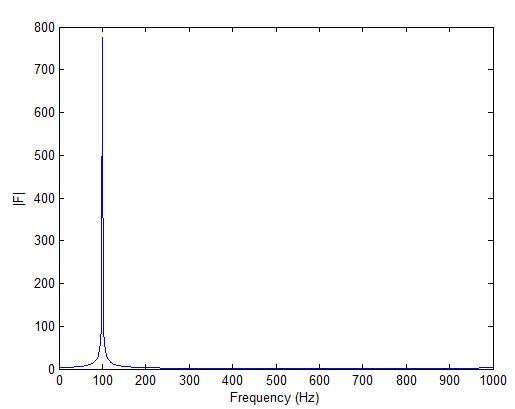
Here we have discussed the case of complex input sequence. Simplifications can be made for a real sequence or for special signals such as pure sine and cosine waves. We will discuss these in later posts.

 [1] Numerical Recipes in C, The Art of Scientific Computing, Cambridge University Press.

Author: Yasir

More than 20 years of experience in various organizations in Pakistan, the USA, and Europe. Worked with the Mobile and Portable Radio Group (MPRG) of Virginia Tech and Qualcomm USA and was one of the first researchers to propose Space Time Block Codes for eight transmit antennas. Have publsihed a book “Recipes for Communication and Signal Processing” through Springer Nature.

Twitter Facebook Linkedin