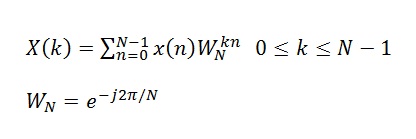Discrete Fourier Transform

Discrete Fourier Transform or DFT is a mathematical operation that transforms a time domain signal to frequency domain. It is usually implemented using the Fast Fourier Transform (FFT). The computational complexity of the DFT is N² whereas its (N)log₂N for the FFT, where N is the number of samples of the the time domain signal. Mathematically, the DFT is written as

and this operation can be easily implemented in MATLAB as shown below.

clear all
close all

fm=100;
fs=1000;
Ts=1/fs;
N=1024;
t=0:Ts:(N-1)*Ts;

x=cos(2*pi*fm*t);
W=exp(-j*2*pi/N);

n=0:N-1;
for k=0:N-1
        X(k+1)=sum(x.*(W.^(k*n)));
end

plot((0:k)/N,abs(X))
xlabel ('Normalized Frequency')
ylabel ('X')

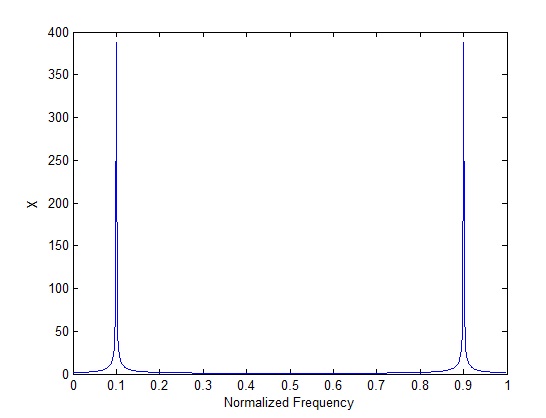
The DFT of the cosine function with frequency of 100Hz is shown below. It must be noted that the frequency in the figure below is normalized by the sampling frequency. So the peaks in the graph occur at 0.1*1000=100Hz and 0.9*1000=900Hz (image frequency). Actually if you zoom in you will see that the peaks are not exactly at 0.1 and 0.9 but  are slightly offset as the frequency bins are not located at exactly those frequencies.

In case of multiple sinusoids the resolution of the DFT becomes important. Higher the sample size (duration of the time domain signal) higher is the resolution of the DFT. As stated earlier the DFT is a computationally complex operation and usually the Fast Fourier Transform (FFT) is used to compute the frequency domain behavior. We will discuss this in the following posts.

A simple way to expedite the process of DFT calculation is to use matrix manipulation instead of a “for loop”.This is shown below.

clear all
close all

fm=100;
fs=1000;
Ts=1/fs;
N=128;
t=0:Ts:(N-1)*Ts;

x=cos(2*pi*fm*t);
W=exp(-j*2*pi/N);

n=0:N-1;
k=0:N-1;

X=x*(W.^(n'*k));

plot(k/N,abs(X))
xlabel ('Normalized Frequency')
ylabel ('X')

Although matrix manipulation makes for a nice and clean code, it was found that there was no improvement in the computation time. Both the “for loop” code and the “matrix multiplication” code took about 0.35 seconds to execute. However, increasing the sample size from 128 to 1024 results in significant better computation time for the latter scheme.

Author: Yasir

More than 20 years of experience in various organizations in Pakistan, the USA, and Europe. Worked with the Mobile and Portable Radio Group (MPRG) of Virginia Tech and Qualcomm USA and was one of the first researchers to propose Space Time Block Codes for eight transmit antennas. Have publsihed a book “Recipes for Communication and Signal Processing” through Springer Nature.

Twitter Facebook Linkedin