Detecting Sinusoids in Noise

We have previously discussed the problem of detecting two closely spaced sinusoids using the Discrete Fourier Transform (DFT). We assumed that the data set we got was pure i.e. there was no noise. However, in reality this is seldom the case. There is always some noise, corrupting the signal. Let us now see how it effects the detection problem.

We consider Additive White Gaussian Noise (AWGN) as the corrupting source. The noise power is set equal to the power of the two sinusoids i.e. we have an SNR of 0 dB. This is quite a severe case, the noise power is usually a few dB below the signal power. We are also bounded by the number of samples, N=64, giving us a resolution of 15.87 Hz.

clear all
close all

fm1=100;
fm2=120;
fs=1000;
Ts=1/fs;
N=64;
t=0:Ts:(N-1)*Ts;

x1=sqrt(2)*cos(2*pi*fm1*t);
x2=sqrt(2)*cos(2*pi*fm2*t);
wn=randn(1,N);
x=x1+x2+wn;
W=exp(-j*2*pi/N);

n=0:N-1;
k=0:N-1;

X=x*(W.^(n'*k));

plot(k/N,20*log10(abs(X)))
xlabel ('Normalized Frequency')
ylabel ('X(dB)')

The data is plotted on a logarithmic scale so that we can compare the signal and noise  power levels.

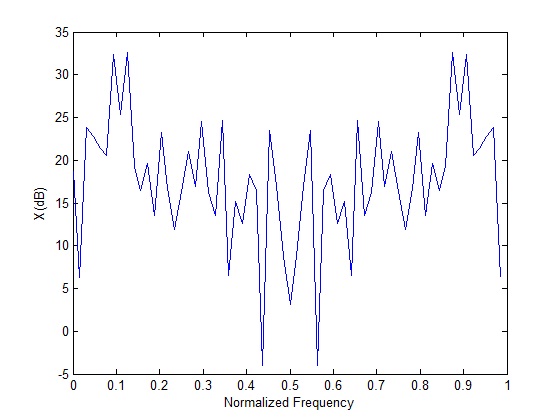
It is observed that we still have two peaks around the required frequency bins but there are also a number of false peaks. These peaks are around 10 dB lower than the signal peaks and should not cause a false detection. So the signal to noise ratio of 0 dB in the time domain is translated to a signal to noise ratio of about 10 dB in the frequency domain (this can be realized using an appropriate filter).

Author: Yasir

More than 20 years of experience in various organizations in Pakistan, the USA, and Europe. Worked with the Mobile and Portable Radio Group (MPRG) of Virginia Tech and Qualcomm USA and was one of the first researchers to propose Space Time Block Codes for eight transmit antennas. Have publsihed a book “Recipes for Communication and Signal Processing” through Springer Nature.

Twitter Facebook Linkedin