So far we have considered the bit error rate (BER) of BPSK and QPSK in an AWGN channel. Now we turn our attention to a Rayleigh fading channel which is a more realistic representation of a wireless communication channel. We consider a single tap Rayleigh fading channel which is good approximation of a flat fading channel i.e. a channel that has flat frequency response (but varying with time). The complex channel coefficient is given as (a+j*b) where a and b are Gaussian random variables with mean 0 and variance 0.5. We use the envelope of this channel coefficient in our simulation as any phase shift is easily removed by the receiver.
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function[ber]=err_rate3(l,EbNo)
si=2*(round(rand(1,l))-0.5);
sq=2*(round(rand(1,l))-0.5);
s=si+j*sq;
n=(1/sqrt(2*10^(EbNo/10)))*(randn(1,l)+j*randn(1,l));
h=(1/sqrt(2))*((randn(1,l))+j*(randn(1,l)));
r=abs(h).*s+n;
si_=sign(real(r));
sq_=sign(imag(r));
ber1=(l-sum(si==si_))/l;
ber2=(l-sum(sq==sq_))/l;
ber=mean([ber1 ber2]);
return
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
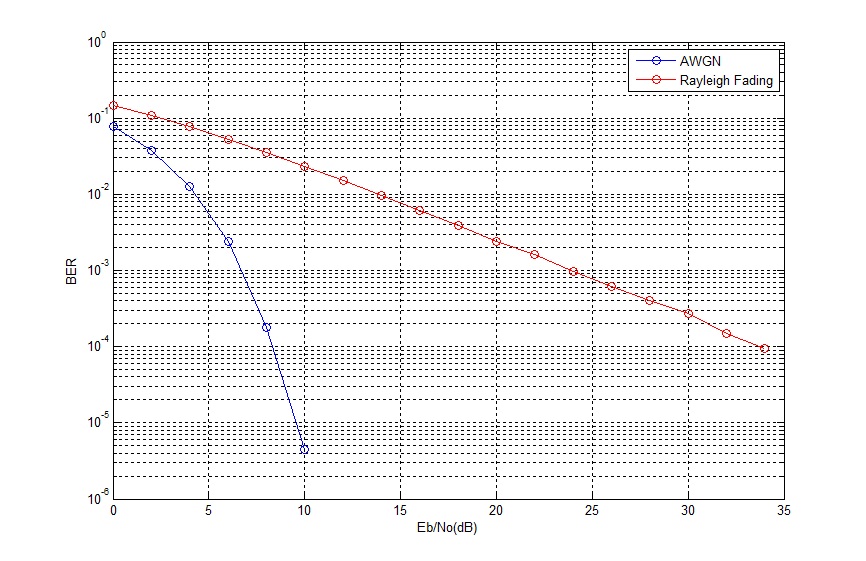
It is observed that the BER for a Rayleigh fading channel is much higher than the BER for an AWGN channel. In fact, for Rayleigh fading, the BER curve is almost a straight line!!!
Note:
1. The input EbNo to the function is in dB so it is converted into linear scale by 10^(EbNo/10).
2. Noise is added in a Rayleigh fading channel as well. Noise is introduced by the receiver front end and is always present.
Author: Yasir
More than 20 years of experience in various organizations in Pakistan, the USA, and Europe. Worked with the Mobile and Portable Radio Group (MPRG) of Virginia Tech and Qualcomm USA and was one of the first researchers to propose Space Time Block Codes for eight transmit antennas. Have publsihed a book “Recipes for Communication and Signal Processing” through Springer Nature.
18 thoughts on “Bit Error Rate of QPSK in Rayleigh Fading”
I have modified the code for including hamming code in QPSK over Rayleigh channel. However, the simulated and theoretical graph are very different. Please check my code and guide me what is wrong in that.
I have not looked at your code as it is quite complex and I need some time for that. But as a start look at the slope of the two curves (theoretical vs simulated)…if they have similar behavior then there is only a calibration issue in your code and it can be adjusted. But if they are intersecting then there is a bigger issue here and you will have to look how you have set up the simulation.
hello.
first, I don’t good in English.
Many people say that “what is variable l?”.
I think that variable l is number of symbols.
So that, if the transmitter want to send the receiver ‘N bit’.
Number of symbols is N/log_2(4)
???????????
hello sir
I want your help. i want matlab code of ber vs snr plot with bpsk,qpsk and 16qam modulation with mrc, egc and sc in mmse sic receiver
Thank you for your answer.
If it is convenient for you , I still have some questions.
How do i know that h is a time varying channel ? Because of using matlab function “randn” ?
In wireless communication simulation , what situation channel coefficient has only one component ( or multiple components )? Does it relate to multiple paths or symbol period ?
I am grateful for your help. Thanks a lot.
Hello. My English is not good but i want to ask some questions. Please help me , thank you .
In above matlab code :
h= (1/sqrt(2))*((randn(1,L))+j*(randn(1,L)));
Is this a multipath Rayleigh channel of number of paths (taps) = L ? I can say that the vector h is a channel impulse response of Rayleigh channel ?
In textbook , i need to convolve transmitted signal with the channel coefficients . Why this code multiply( .* ) transmitted signal for the channel coefficients h ?
In this conent ,
( http://www.raymaps.com/index.php/ber-of-64-qam-ofdm-in-fading/ )
ht=[0.8 0.54 0.24 0.10 0.04] is a simple FIR filter for channel model with coefficients . what is difference between ht and h= (1/sqrt(2))*((randn(1,L))+j*(randn(1,L))) ? What is that Physical meaning ?
Please help me. I have search many information on the Web but i am still confused. Thanks.
ht is a static channel model, coefficients are not changing with time, h is a time varying channel where coefficients are Rayleigh distributed (the real and imaginary parts have normal distribution). Yes, the channel must be convolved with the signal.
Furthermore, ht is a frequency selective channel or in time domain you can say it causes Intersymbol Interference (ISI) due to multiple taps just like an FIR filter. Whereas, h is a flat channel as it has just one tap per time instant. The signal is convolved with ht and multiplied by h.
When channel has only one component (that is FIR filter has only one coefficient) convolution in equivalent to multiplication. Such is the case when the symbol period is much longer than the channel length (in time).
i need the complete code
You just need to call the function for each value of signal to noise ratio that you intend to simulate.
Basco: The bit error rate of BPSK and QPSK is the same. It is the the symbol error rate that is different. I only plot the BER here.
QPSK is actually two orthogonal BPSK signals carrying one bit each, so the BER should be same.
I think your theoretical curve is wrong.
At SNR=25, QPSK BER should be slightly above 10^-3
Your result matches that of BPSK
see second graph in the link http://www.dsplog.com/2008/09/19/equal-gain-combining/
Hi John Could you please tell me how to Perform Simulation of Outage Probability. Do we have to find Empirical Distribution?
First you need to decide on a distribution for the signal envelope, such as Rayleigh distribution. Then select on a threshold. Integrate the distribution function from zero to the threshold. This would give you the outage probability for the given distribution and given threshold.
Hope this helps!
what is variable ‘l’ in the matlab code?
Madhoori: It is the number of symbols to be passed through the channel. It should be large enough to get accurate results but not so large that the simulation takes forever. A good value of ‘l’ is that which gives us 20-25 errors. So a few million symbols need to be passed at high SNR to get accurate results.