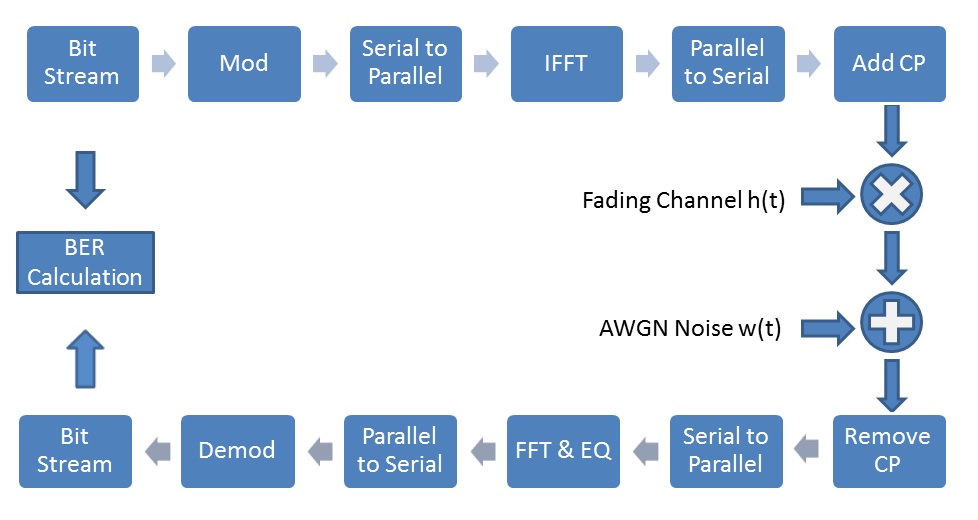
As the data rates supported by wireless networks continue to rise the bandwidth requirements also continue to increase (although spectral efficiency has also improved). Remember GSM technology which supported 125 channels of 200KHz each, which was further divided among eight users using TDMA. Move on to LTE where the channel bandwidth could be as high as 20MHz (1.4MHz, 3MHz, 5MHz, 10MHz, 15MHz and 20MHz are standardized).
This advancement poses a unique challenge referred to as frequency selective fading. This means that different parts of the signal spectrum would see a different channel (different amplitude and different phase offset). Look at this in the time domain where the larger bandwidth means shorter symbol period causing intersymbol interference (as time delayed copies of the signal overlap on arrival at the receiver).
The solution to this problem is OFDM that divides the wideband signal into smaller components each having a bandwidth of a few KHz. Each of these components experiences a flat channel. To make the task of equalization simple a cyclic prefix (CP) is added in the time domain to make the effect of fading channel appear as circular convolution. Thus simplifying the frequency domain equalization to a simple division operation.
Shown below is the Python code that calculates the bit error rate (BER) of BPSK-OFDM which is the same as simple BPSK in a Rayleigh flat fading channel. However there is a caveat. We have inserted a CP which means we are transmitting more energy than simple BPSK. To be exact we are transmitting 1.25 (160/128) times more energy. This means that if this excess energy is accounted for the performance of BPSK-OFDM would be 1dB (10*log10(1.25)) worse than simple BPSK in Rayleigh flat fading channel.
Note:
- Although we have shown the channel as a multiplicative effect in the figure above, this is only true for a single tap channel. For a multi-tap channel (such as the one used in the code above) the effect of the channel is that of a filter which performs convolution operation on the transmitted signal.
- We have used a baseband model in our simulation and the accompanying figure. In reality the transmitted signal is upconverted before transmission by the antennas.
- The above model can be easily modified for any modulation scheme such as QPSK or 16-QAM. The main difference would be that the signal would have a both a real part and an imaginary part, much of the simulation would remain the same. This would be the subject of a future post. For a MATLAB implementation of 64-QAM OFDM see the following post (64-QAM OFDM).
- Serial to parallel and parallel to serial conversion shown in the above figure was not required as the simulation was done symbol by symbol (one OFDM symbol in the time domain represented 128 BPSK symbols in the frequency domain).
- The channel model in the above simulation is quasi-static i.e. it remains constant for one OFDM symbol but then rapidly changes for the next, without any memory.