Introduction
A Uniform Linear Array (ULA) is a collection of sensor elements equally spaced along a straight line. The most common type of sensor is a dipole antenna that can transmit and receive Electromagnetic Waves over the air. Other types of sensors include acoustic sensors that may be used in air or under water. The requirements of a ULA are different for different applications but the most common requirement is to improve the Signal to Noise Ratio (SNR) and to improve its response (Gain) in a particular direction. The second property means that the array accepts a signal from a particular direction and rejects the signal from another direction just as required in Radar.
Excess Path Length
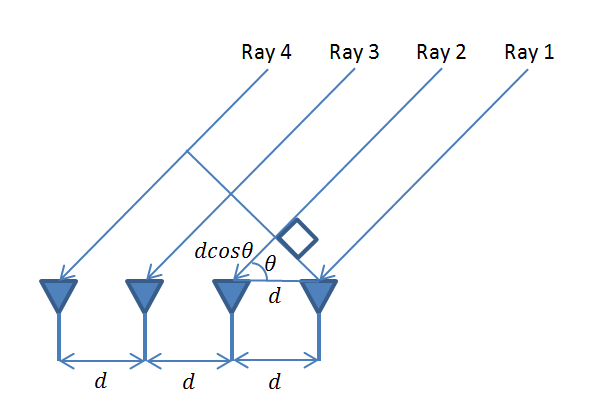
The graphical representation and the mathematical framework for the problem are shown below. It is assumed that Electromagnetic Waves (Rays) arrive at the array in the form of a plane wave. This means that there is a large distance between the transmitter and receiver (the receiver is in the far field of the transmitter). The array elements are separated by a distance ‘d’ which must be less than or equal to half the wavelength (similar to the concept of minimum sampling frequency in DSP). Now we can see that the second ray travels an excess distance dcos(θ). Similarly, the third and fourth rays travel an excess distance of 2dcos(θ) and 3dcos(θ) respectively. In array processing it is this excess distance between the arriving rays that is important, absolute distance from the source does not matter (unless you are interested in large scale effects such as path loss). This excess distance between the different rays determines if the signals are going to add constructively or destructively.
Mathematical Model of a ULA
Simulation Methodology
Given below is the MATLAB code for the scenario shown in the figure above. We have considered two methods, one employing a ‘for-loop’ and another using matrix manipulation. The second method is usually preferred as it is much faster and also allows us to directly apply techniques from linear estimation theory. We have plotted the array pattern for four cases with N=2,4,6 and 8. It is seen that as the number of array elements increases the Gain (or Directivity) of the array increases. In the case shown below we have considered that the four received signals are added with equal weights (w=1), but these weights can be adjusted to get various beam patterns (weights are typically complex quantities adjusting both phase and amplitude of the signal). This is typically called Beamforming and we will discuss this in a future post.
Matlab Code
FOR LOOP IMPLEMENTATION
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% SIMPLE UNIFORM LINEAR ARRRAY
% WITH VARIABLE NUMBER OF ELEMENTS
% COPYRIGHT RAYMAPS (C) 2018
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clear all
close all
f=1e9;
c=3e8;
l=c/f;
d=l/2;
no_elements=4;
theta=0:pi/180:2*pi;
r=zeros(1,length(theta));
for n=1:no_elements
dx(n,:)=(n-1)*d*cos(theta);
r=r+exp(-i*2*pi*(dx(n,:)/l));
end
polar(theta,abs(r),'b')
title ('Gain of a Uniform Linear Array')
MATRIX IMPLEMENTATION
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% SIMPLE UNIFORM LINEAR ARRRAY
% WITH VARIABLE NUMBER OF ELEMENTS
% MATRIX IMPLEMENTATION
% COPYRIGHT RAYMAPS (C) 2018
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clear all
close all
f=1e9;
c=3e8;
l=c/f;
d=l/2;
no_elements=4;
theta=0:pi/180:2*pi;
n=1:no_elements;
n=transpose(n);
A=(n-1)*(i*2*pi*d*cos(theta)/l);
X=exp(-A);
w=ones(1,no_elements);
r=w*X;
polar(theta,abs(r),'r')
title ('Gain of a Uniform Linear Array')
MATLAB Plot
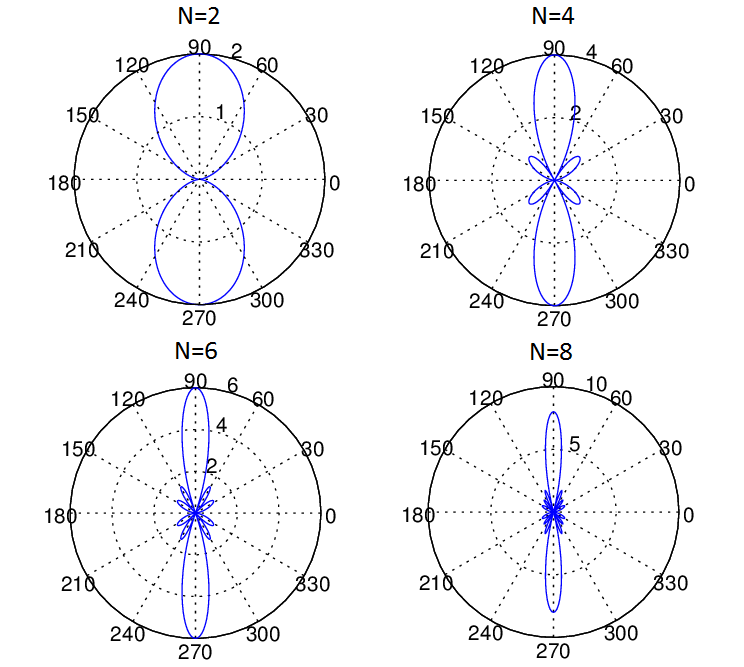
Note: For a Uniform Linear Array with N elements and half wavelength inter-element spacing the Half Power Beam Width (HPBW) can be estimated as 1.78/N Radians [source]. For the four element case shown above the formula gave a HPBW of 25.49 degrees whereas our simulation yielded 26.20 degrees. For ten element case the formula gave a HPBW of 10.19 degrees whereas the simulation result was 10.20 degrees. Similarly the result for 20 elements is also quite accurate. So we can say that the formula does help us to get a ballpark estimate and gives progressively more accurate results as the number of elements is increased. For a general case where the inter-element spacing is not equal to half wavelength the formula is 0.89*(wavelength/total aperture length).
Lastly, for those who still do not know what Half Power Beam Width also known as 3dB Bandwidth means, it is the width of the main lobe in degrees 3dB down from the peak value of the radiation pattern.