In the previous post we had introduced the Discrete Fourier Transform (DFT) as a method to perform the spectral analysis of a time domain signal. We now discuss an important property of the DFT, its spectral resolution i.e. its ability to resolve two signals with similar spectral content.
Initially one might think that increasing the sampling frequency would increase the spectral resolution but this totally incorrect. In fact if the sampling frequency is increased, keeping the number of time domain samples to be the same, the resolution actually decreases. So how do we calculate the spectral resolution. One simple way is to calculate the difference between two frequency bins as fs/(N-1) or 1/(N-1)Ts. Simply put the resolution in the frequency domain is the inverse of the sample length in the time domain.
So let us now calculate the DFT of two closely spaced sine waves keeping the sampling frequency to be the same and changing the number of time domain samples (only the result for N=64 shown here). We again list down the code used to calculate the DFT.
clear all
close all
fm1=100;
fm2=120;
fs=1000;
Ts=1/fs;
N=64;
t=0:Ts:(N-1)*Ts;
x1=cos(2*pi*fm1*t);
x2=cos(2*pi*fm2*t);
x=x1+x2;
W=exp(-j*2*pi/N);
n=0:N-1;
k=0:N-1;
X=x*(W.^(n'*k));
plot(k/N,abs(X))
xlabel ('Normalized Frequency')
ylabel ('X')
We first do some quick math to find the spectral resolution.
fs/(N-1)=1000/(64-1)=15.87 Hz
Now the two tones are space 20 Hz apart (100 Hz and 120 Hz), so we can predict that the two tones would be detected successfully. The result of the DFT operation on the composite signal is shown below.
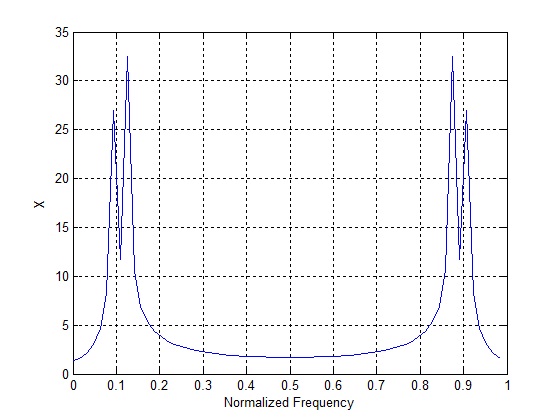
It is observed that although the two tones are detected, they are not exactly at the desired frequencies (0.10 and 0.12). Secondly the amplitude of the two tones is different although the time domain signals had equal amplitude. Both these phenomenon are due to the fact that we only have a limited number of frequency bins (N=64) due to which the resulting spectrum is only an estimate of the true spectrum.
There are better techniques than DFT to separate two closely spaced sinusoids and these are known as super resolution spectral techniques and would be discussed some other time.
Author: Yasir Ahmed (aka John)
More than 20 years of experience in various organizations in Pakistan, the USA, and Europe. Worked as a Research Assistant within the Mobile and Portable Radio Group (MPRG) of Virginia Tech and was one of the first researchers to propose Space Time Block Codes for eight transmit antennas. The collaboration with MPRG continued even after graduating with an MSEE degree and has resulted in 12 research publications and a book on Wireless Communications. Worked for Qualcomm USA as an Engineer with the key role of performance and conformance testing of UMTS modems. Qualcomm is the inventor of CDMA technology and owns patents critical to the 4G and 5G standards.