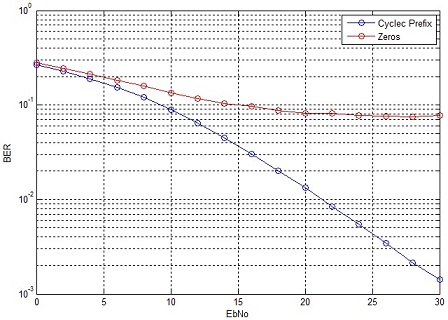
Have you ever thought that Cyclic Prefix in OFDM is just a gimmick and we could do equally well by using a guard period i.e. a period of no transmission between two OFDM symbols. Well, one way to find out if this is true is by running a bit error rate simulation with and without a cyclic prefix (only a vacant guard period). We use the 64-QAM OFDM simulation that we developed previously. The channel is modeled as 7-tap FIR filter with each tap having a Rayleigh distribution.
We simulate the case of a vacant guard period by inserting zeros in the time slot dedicated for the CP (32 samples). It is observed that there is a vast difference in the bit error rate (BER) for the two cases. In fact in the case of no CP the BER hits an error floor at around 20 dB. Increasing the signal to noise ratio does not improve the BER performance any further.
Now to answer the question “why does the CP work” we have to revisit the concept of circular convolution from our DSP course. It is well known that performing circular convolution of two sequences in the time domain is equivalent to multiplication of their DFT’s in the frequency domain. So if a wireless channel performed circular convolution we could do simple division to recover the signal after the FFT operation in the receiver.
Y(k)=X(k)*H(k) Effect of Wireless Channel
X(k)=Y(k)/H(k) Recovery of the Signal
But the wireless channel does not perform circular convolution, it performs linear convolution. So the trick is to make this linear convolution appear as circular convolution by appending a cyclic prefix. The result is that equalization can be performed at the receiver by simple division.
For a more elaborate discussion on this you may visit CP-1 or for a mathematical description you may visit CP-2.
Note: In a actual system there would be AWGN noise added to the received signal as well. Giving us the following relationships.
Y(k)=X(k)*H(k)+W(k) Effect of Wireless Channel
X(k)’=Y(k)/H(k)=X(k)+W(k)/H(k) Recovery of the Signal
Author: Yasir Ahmed (aka John)
More than 20 years of experience in various organizations in Pakistan, the USA, and Europe. Worked as a Research Assistant within the Mobile and Portable Radio Group (MPRG) of Virginia Tech and was one of the first researchers to propose Space Time Block Codes for eight transmit antennas. The collaboration with MPRG continued even after graduating with an MSEE degree and has resulted in 12 research publications and a book on Wireless Communications. Worked for Qualcomm USA as an Engineer with the key role of performance and conformance testing of UMTS modems. Qualcomm is the inventor of CDMA technology and owns patents critical to the 4G and 5G standards.
It is also possible to ‘mimic’ a circular convolution by taking doing a “prefix-like” operation at the receiver side. Take the received samples corresponding to the guard period -containing some information about the end of the signal- and add these to the samples corresponding to the beginning of the symbol. In the absence of noise, the results are identical. Also inthe presence of noise, the performance would not be very different. Maybe doing this step at the receiver would make for a fairer comparison.
Kudos for these nonetheless very informative pages!
Gert,
This is a very innovative idea…would look into this further. Thanks for sharing!
John
Peter,
Yes you can simulate different CP lengths. My simulation actually penalizes you for the longer CP since you are transmitting more energy per “useful bit”. So you may see a degradation in performance. But also remember that I am using a 7-tap FIR filter to model the channel. A longer CP would become really useful when the channel length is longer.
Hope this helps…
John
Hello.
From your code, is it possible to simulate the result with different CP length ?
The results shows that when increasing the CP length, the BER performance actually degrades.
Is it correct?
Thank you very much.
Pretty insightful. Thanks!
My site:
telefon dsl vergleich oder DSL anbieter